| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Solved Examples (Examples 1 to 16) | Question 1 to 25 (Multiple Choice Questions) | Question 26 to 47 (Fill in the Blanks) |
| Question 48 to 99 (True or False) | Question 100 to 152 | |
Chapter 1 Rational Numbers
Welcome to this comprehensive resource providing detailed, step-by-step solutions for the NCERT Exemplar problems specifically designed for Class 8 Mathematics, Chapter 1: Rational Numbers. It is crucial to understand that these Exemplar questions are crafted to push students beyond the basic definitions and operations typically found in standard textbooks. They aim to significantly deepen conceptual understanding by exploring the intricate properties and diverse applications of rational numbers within more challenging and thought-provoking contexts, thereby building a stronger foundation in number systems and algebra.
The solutions meticulously address the core concepts underpinning rational numbers. This begins with the fundamental definition: any number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and the denominator $q$ is explicitly not equal to zero ($q \neq 0$). Key aspects covered include finding equivalent rational numbers, reducing them to their standard form (where $q > 0$ and $p, q$ are co-prime), representing rational numbers accurately on the number line, and comparing their values, often involving negative numbers where careful handling is essential.
A primary focus of the Exemplar problems, and consequently these solutions, is the thorough exploration of the properties of rational numbers under the operations of addition and multiplication. Understanding these properties is key not just for computation but for appreciating the algebraic structure of this number system. The solutions clearly demonstrate:
- Closure Property: Are rational numbers closed under addition, subtraction, multiplication, division (excluding division by zero)?
- Commutativity: Does order matter? Is $\frac{a}{b} + \frac{c}{d} = \frac{c}{d} + \frac{a}{b}$ and $\frac{a}{b} \times \frac{c}{d} = \frac{c}{d} \times \frac{a}{b}$?
- Associativity: Does grouping matter? Is $(\frac{a}{b} + \frac{c}{d}) + \frac{e}{f} = \frac{a}{b} + (\frac{c}{d} + \frac{e}{f})$ and $(\frac{a}{b} \times \frac{c}{d}) \times \frac{e}{f} = \frac{a}{b} \times (\frac{c}{d} \times \frac{e}{f})$?
- Role of Identities: Understanding $0$ as the Additive Identity ($\frac{p}{q} + 0 = \frac{p}{q}$) and $1$ as the Multiplicative Identity ($\frac{p}{q} \times 1 = \frac{p}{q}$).
- Existence of Inverses: Recognizing the Additive Inverse (for $\frac{p}{q}$, it's $-\frac{p}{q}$) and the Multiplicative Inverse or Reciprocal (for non-zero $\frac{p}{q}$, it's $\frac{q}{p}$).
- The vital Distributive Property of multiplication over addition: $\frac{a}{b} \times (\frac{c}{d} + \frac{e}{f}) = (\frac{a}{b} \times \frac{c}{d}) + (\frac{a}{b} \times \frac{e}{f})$. Exemplar problems frequently demand the strategic application of this property to simplify complex numerical expressions efficiently, rather than relying solely on brute-force calculation following BODMAS rules.
Other important concepts addressed include illustrating the density property of rational numbers – the fact that between any two distinct rational numbers, there exist infinitely many other rational numbers. The solutions guide through methods for finding one or multiple rational numbers lying between two given ones. The solutions cater to diverse question formats including MCQs testing precise understanding, Fill-in-the-Blanks, True/False statements probing conceptual clarity (e.g., addressing properties like division not being commutative or associative), and comprehensive Short/Long Answer questions. These often require detailed simplification using properties, solving multi-step word problems involving fractional quantities, or verifying properties through specific examples. The provided solutions offer crystal-clear explanations for each step, explicitly highlighting the property being used for simplification, ensuring accurate calculations (especially with signs and fractions), and providing logical breakdowns for word problems. This resource is invaluable for students aiming to achieve genuine mastery over rational numbers, understand their fundamental algebraic structure, and confidently apply these concepts to solve complex mathematical problems.
Solved Examples (Examples 1 to 16)
In examples 1 to 3, there are four options out of which one is correct. Choose the correct answer.
Example 1: Which of the following is not true?
(a) $\frac{2}{3}$ + $\frac{5}{4}$ = $\frac{5}{4}$ + $\frac{2}{3}$
b) $\frac{2}{3}$ - $\frac{5}{4}$ = $\frac{5}{4}$ - $\frac{2}{3}$
(c) $\frac{2}{3}$ × $\frac{5}{4}$ = $\frac{5}{4}$ × $\frac{2}{3}$
(d) $\frac{2}{3}$ ÷ $\frac{5}{4}$ = $\frac{2}{3}$ × $\frac{4}{5}$
Answer:
We are asked to find the statement that is not true among the given options.
Let's examine each option:
Option (a): $\frac{2}{3} + \frac{5}{4}$.
Adding the fractions: $\frac{2}{3} + \frac{5}{4} = \frac{2 \times 4}{3 \times 4} + \frac{5 \times 3}{4 \times 3} = \frac{8}{12} + \frac{15}{12} = \frac{8+15}{12} = \frac{23}{12}$.
Now, $\frac{5}{4} + \frac{2}{3}$.
Adding the fractions: $\frac{5}{4} + \frac{2}{3} = \frac{5 \times 3}{4 \times 3} + \frac{2 \times 4}{3 \times 4} = \frac{15}{12} + \frac{8}{12} = \frac{15+8}{12} = \frac{23}{12}$.
Since $\frac{23}{12} = \frac{23}{12}$, the statement $\frac{2}{3} + \frac{5}{4} = \frac{5}{4} + \frac{2}{3}$ is true. This demonstrates the commutative property of addition for rational numbers.
Option (b): $\frac{2}{3} - \frac{5}{4}$.
Subtracting the fractions: $\frac{2}{3} - \frac{5}{4} = \frac{2 \times 4}{3 \times 4} - \frac{5 \times 3}{4 \times 3} = \frac{8}{12} - \frac{15}{12} = \frac{8-15}{12} = -\frac{7}{12}$.
Now, $\frac{5}{4} - \frac{2}{3}$.
Subtracting the fractions: $\frac{5}{4} - \frac{2}{3} = \frac{5 \times 3}{4 \times 3} - \frac{2 \times 4}{3 \times 4} = \frac{15}{12} - \frac{8}{12} = \frac{15-8}{12} = \frac{7}{12}$.
Since $-\frac{7}{12} \neq \frac{7}{12}$, the statement $\frac{2}{3} - \frac{5}{4} = \frac{5}{4} - \frac{2}{3}$ is not true. Subtraction is not commutative for rational numbers in general.
Option (c): $\frac{2}{3} \times \frac{5}{4}$.
Multiplying the fractions: $\frac{2}{3} \times \frac{5}{4} = \frac{2 \times 5}{3 \times 4} = \frac{10}{12} = \frac{5}{6}$.
Now, $\frac{5}{4} \times \frac{2}{3}$.
Multiplying the fractions: $\frac{5}{4} \times \frac{2}{3} = \frac{5 \times 2}{4 \times 3} = \frac{10}{12} = \frac{5}{6}$.
Since $\frac{5}{6} = \frac{5}{6}$, the statement $\frac{2}{3} \times \frac{5}{4} = \frac{5}{4} \times \frac{2}{3}$ is true. This demonstrates the commutative property of multiplication for rational numbers.
Option (d): $\frac{2}{3} \div \frac{5}{4} = \frac{2}{3} \times \frac{4}{5}$.
This statement is the definition of division of rational numbers. Dividing by a fraction is equivalent to multiplying by its reciprocal. This statement is true.
Based on the evaluation of each option, the statement that is not true is option (b).
The correct answer is (b).
Example 2: Multiplicative inverse of $\frac{0}{1}$ is
(a) 1
(b) –1
(c) 0
(d) not defined
Answer:
The given number is $\frac{0}{1}$.
Simplifying the fraction, we get: $\frac{0}{1} = 0$.
We need to find the multiplicative inverse of 0.
The multiplicative inverse of a rational number $a$ (where $a \neq 0$) is $\frac{1}{a}$, such that $a \times \frac{1}{a} = 1$.
In general, for any number $x$, its multiplicative inverse $y$ is such that $x \times y = 1$.
We are looking for the multiplicative inverse of 0. Let this inverse be $y$.
According to the definition, we must have:
$0 \times y = 1$
However, the product of 0 and any number is always 0.
So, $0 \times y = 0$ for any value of $y$.
This means that the equation $0 \times y = 1$ has no solution, as $0$ is not equal to $1$.
Therefore, there is no number $y$ that can be multiplied by 0 to get 1.
Hence, the multiplicative inverse of 0 is not defined.
The multiplicative inverse of $\frac{0}{1}$ (which is 0) is not defined.
The correct option is (d).
Example 3: Three rational numbers lying between $\frac{-3}{4}$ and $\frac{1}{2}$ are
(a) $\frac{-1}{2}$ , 0, $\frac{3}{4}$
(b) $\frac{-1}{4}$ , $\frac{1}{4}$ , $\frac{3}{4}$
(c) $\frac{-1}{4}$ , 0 , $\frac{1}{4}$
(d) $\frac{-5}{4}$ , 0 , $\frac{1}{4}$
Answer:
Given:
Two rational numbers are $\frac{-3}{4}$ and $\frac{1}{2}$.
To Find:
Three rational numbers lying between $\frac{-3}{4}$ and $\frac{1}{2}$.
Solution:
To find rational numbers between two given rational numbers, it is helpful to express them with a common denominator.
The denominators are 4 and 2. The Least Common Multiple (LCM) of 4 and 2 is 4.
Let's write both fractions with the denominator 4:
The first fraction is already $\frac{-3}{4}$.
For the second fraction, $\frac{1}{2}$, we multiply the numerator and denominator by 2:
$\frac{1}{2} = \frac{1 \times 2}{2 \times 2} = \frac{2}{4}$
Now we need to find three rational numbers between $\frac{-3}{4}$ and $\frac{2}{4}$.
We can look for rational numbers with denominator 4 whose numerators are integers between -3 and 2.
The integers between -3 and 2 are -2, -1, 0, 1.
So, some rational numbers between $\frac{-3}{4}$ and $\frac{2}{4}$ are $\frac{-2}{4}$, $\frac{-1}{4}$, $\frac{0}{4}$, $\frac{1}{4}$.
Simplifying these fractions, we get:
$\frac{-2}{4} = -\frac{1}{2}$
$\frac{-1}{4}$
$\frac{0}{4} = 0$
$\frac{1}{4}$
So, rational numbers like $-\frac{1}{2}$, $-\frac{1}{4}$, 0, $\frac{1}{4}$ lie between $\frac{-3}{4}$ and $\frac{1}{2}$.
Now let's check the given options to see which one contains three numbers from this list or three numbers that fall within the range $\left(\frac{-3}{4}, \frac{1}{2}\right)$.
Range: $(-0.75, 0.5)$.
Option (a): $\frac{-1}{2} = -0.5$, $0$, $\frac{3}{4} = 0.75$. $\frac{3}{4}$ is greater than $\frac{1}{2}$, so this option is incorrect.
Option (b): $\frac{-1}{4} = -0.25$, $\frac{1}{4} = 0.25$, $\frac{3}{4} = 0.75$. $\frac{3}{4}$ is greater than $\frac{1}{2}$, so this option is incorrect.
Option (c): $\frac{-1}{4} = -0.25$, $0$, $\frac{1}{4} = 0.25$. All these numbers are between $\frac{-3}{4} (-0.75)$ and $\frac{1}{2} (0.5)$.
$-0.75 < -0.25 < 0.5$
$-0.75 < 0 < 0.5$
$-0.75 < 0.25 < 0.5$
So, option (c) contains three rational numbers lying between $\frac{-3}{4}$ and $\frac{1}{2}$.
Option (d): $\frac{-5}{4} = -1.25$, $0$, $\frac{1}{4} = 0.25$. $\frac{-5}{4}$ is less than $\frac{-3}{4}$, so this option is incorrect.
The three rational numbers lying between $\frac{-3}{4}$ and $\frac{1}{2}$ are $\frac{-1}{4}$, 0, and $\frac{1}{4}$.
The correct answer is (c).
In examples 4 and 5, fill in the blanks to make the statements true.
Example 4: The product of a non-zero rational number and its reciprocal is ________.
Answer:
Let the non-zero rational number be $x$.
Since $x$ is a non-zero rational number, its reciprocal is $\frac{1}{x}$.
The product of the rational number and its reciprocal is given by:
$\text{Product} = x \times \frac{1}{x}$
Multiplying $x$ by $\frac{1}{x}$:
$\text{Product} = \frac{x}{1} \times \frac{1}{x} = \frac{x \times 1}{1 \times x} = \frac{x}{x}$
Since $x$ is a non-zero rational number, $x \neq 0$. Therefore, $\frac{x}{x} = 1$.
$\text{Product} = 1$
This is a fundamental property of reciprocals.
The product of a non-zero rational number and its reciprocal is 1.
The completed statement is: The product of a non-zero rational number and its reciprocal is 1.
Example 5: If x = $\frac{1}{3}$ and y = $\frac{6}{7}$ then xy - $\frac{y}{x}$ = _______.
Answer:
Given:
$x = \frac{1}{3}$
$y = \frac{6}{7}$
To Find:
The value of the expression $xy - \frac{y}{x}$.
Solution:
First, let's calculate the product $xy$:
$xy = \frac{1}{3} \times \frac{6}{7}$
$= \frac{1 \times 6}{3 \times 7} = \frac{6}{21}$
Simplifying the fraction $\frac{6}{21}$ by dividing the numerator and denominator by their greatest common divisor, which is 3:
$\frac{6}{21} = \frac{\cancel{6}^{2}}{\cancel{21}_{7}} = \frac{2}{7}$
So, $xy = \frac{2}{7}$.
Next, let's calculate the division $\frac{y}{x}$:
$\frac{y}{x} = \frac{\frac{6}{7}}{\frac{1}{3}}$
Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of $\frac{1}{3}$ is $\frac{3}{1}$.
$\frac{y}{x} = \frac{6}{7} \times \frac{3}{1}$
$= \frac{6 \times 3}{7 \times 1} = \frac{18}{7}$
So, $\frac{y}{x} = \frac{18}{7}$.
Now, substitute these values into the expression $xy - \frac{y}{x}$:
$xy - \frac{y}{x} = \frac{2}{7} - \frac{18}{7}$
Since the fractions have a common denominator, we can subtract the numerators:
$= \frac{2 - 18}{7}$
$= \frac{-16}{7}$
Thus, if $x = \frac{1}{3}$ and $y = \frac{6}{7}$, then $xy - \frac{y}{x} = \frac{-16}{7}$.
The completed statement is: If x = $\frac{1}{3}$ and y = $\frac{6}{7}$ then xy - $\frac{y}{x}$ = $\frac{-16}{7}$.
In examples 6 and 7, state whether the given statements are true or false.
Example 6: Every rational number has a reciprocal.
Answer:
The statement is False.
A rational number is a number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
The reciprocal of a non-zero rational number $\frac{p}{q}$ is $\frac{q}{p}$, provided $p \neq 0$. The product of a number and its reciprocal is 1.
For example, the reciprocal of $\frac{2}{3}$ is $\frac{3}{2}$, and $\frac{2}{3} \times \frac{3}{2} = 1$.
Consider the rational number 0. Zero can be written as $\frac{0}{1}$.
If 0 had a reciprocal, let's call it $r$. Then, according to the definition of a reciprocal, the product of 0 and $r$ must be 1.
$0 \times r = 1$
However, the product of 0 and any number is always 0.
$0 \times r = 0$
Since $0 \neq 1$, there is no number $r$ such that $0 \times r = 1$.
Therefore, the rational number 0 does not have a reciprocal.
Since there exists at least one rational number (namely 0) that does not have a reciprocal, the statement "Every rational number has a reciprocal" is false.
Example 7: $\frac{-4}{5}$ is larger than $\frac{-5}{4}$ .
Answer:
We need to compare the two rational numbers $\frac{-4}{5}$ and $\frac{-5}{4}$ and determine if the statement "$\frac{-4}{5}$ is larger than $\frac{-5}{4}$" is true.
To compare fractions, we can find a common denominator. The denominators are 5 and 4.
The Least Common Multiple (LCM) of 5 and 4 is $5 \times 4 = 20$.
Now, we convert both fractions to equivalent fractions with a denominator of 20:
$\frac{-4}{5} = \frac{-4 \times 4}{5 \times 4} = \frac{-16}{20}$
$\frac{-5}{4} = \frac{-5 \times 5}{4 \times 5} = \frac{-25}{20}$
Now we need to compare $\frac{-16}{20}$ and $\frac{-25}{20}$.
When comparing fractions with the same denominator, the fraction with the larger numerator is the larger fraction.
We need to compare the numerators -16 and -25.
On the number line, -16 is to the right of -25.
$-16 > -25$
Therefore, $\frac{-16}{20}$ is larger than $\frac{-25}{20}$.
$\frac{-16}{20} > \frac{-25}{20}$
Substituting the original fractions back:
$\frac{-4}{5} > \frac{-5}{4}$
This means that $\frac{-4}{5}$ is indeed larger than $\frac{-5}{4}$.
The statement "$\frac{-4}{5}$ is larger than $\frac{-5}{4}$" is True.
Example 8: Find $\frac{4}{7}$ × $\frac{14}{3}$ ÷ $\frac{2}{3}$
Answer:
Given:
The expression $\frac{4}{7} \times \frac{14}{3} \div \frac{2}{3}$.
To Find:
The value of the given expression.
Solution:
We need to evaluate the expression $\frac{4}{7} \times \frac{14}{3} \div \frac{2}{3}$.
According to the order of operations, we perform multiplication and division from left to right. Alternatively, we can first convert all division operations into multiplication by the reciprocal of the divisor.
The expression is $\frac{4}{7} \times \frac{14}{3} \div \frac{2}{3}$.
The reciprocal of $\frac{2}{3}$ is $\frac{3}{2}$.
So, the expression becomes:
$\frac{4}{7} \times \frac{14}{3} \times \frac{3}{2}$
Now, we multiply the numerators together and the denominators together:
$= \frac{4 \times 14 \times 3}{7 \times 3 \times 2}$
We can cancel the common factors in the numerator and the denominator before multiplying completely. The common factors are 3, 7 (which is a factor of 14), and 2 (which is a factor of 4 and 14).
Cancelling the common factors:
$= \frac{\cancel{4}^{2} \times \cancel{14}^{2} \times \cancel{3}^{1}}{\cancel{7}^{1} \times \cancel{3}^{1} \times \cancel{2}^{1}}$
Multiply the remaining factors in the numerator and the denominator:
$= \frac{2 \times 2 \times 1}{1 \times 1 \times 1} = \frac{4}{1} = 4$
The value of the expression $\frac{4}{7} \times \frac{14}{3} \div \frac{2}{3}$ is 4.
Example 9: Using appropriate properties, find $\frac{2}{3}$ × $\frac{-5}{7}$ + $\frac{7}{3}$ + $\frac{2}{3}$ × $\frac{-2}{7}$ .
Answer:
Given:
The expression $\frac{2}{3} \times \frac{-5}{7} + \frac{7}{3} + \frac{2}{3} \times \frac{-2}{7}$.
To Find:
The value of the given expression using appropriate properties.
Solution:
The given expression is:
$\frac{2}{3} \times \frac{-5}{7} + \frac{7}{3} + \frac{2}{3} \times \frac{-2}{7}$
We can rearrange the terms using the commutative property of addition ($a + b = b + a$).
Rearranging the terms to group the multiplication parts:
$= \frac{2}{3} \times \frac{-5}{7} + \frac{2}{3} \times \frac{-2}{7} + \frac{7}{3}$
Now, we can observe that the term $\frac{2}{3}$ is common in the first two terms. We can use the distributive property of multiplication over addition ($a \times b + a \times c = a \times (b+c)$).
Let $a = \frac{2}{3}$, $b = \frac{-5}{7}$, and $c = \frac{-2}{7}$.
$= \frac{2}{3} \times \left(\frac{-5}{7} + \frac{-2}{7}\right) + \frac{7}{3}$
First, calculate the sum inside the parenthesis. Since the fractions have the same denominator, we add the numerators:
$\frac{-5}{7} + \frac{-2}{7} = \frac{-5 + (-2)}{7} = \frac{-5 - 2}{7} = \frac{-7}{7}$
$\frac{-7}{7} = -1$
Now, substitute this back into the expression:
$= \frac{2}{3} \times (-1) + \frac{7}{3}$
Perform the multiplication:
$\frac{2}{3} \times (-1) = \frac{2 \times (-1)}{3} = \frac{-2}{3}$
The expression is now:
$= \frac{-2}{3} + \frac{7}{3}$
Now, perform the addition. Since the fractions have the same denominator, we add the numerators:
$= \frac{-2 + 7}{3}$
$= \frac{5}{3}$
The value of the expression $\frac{2}{3} \times \frac{-5}{7} + \frac{7}{3} + \frac{2}{3} \times \frac{-2}{7}$ is $\frac{5}{3}$.
Example 10: Let O, P and Z represent the numbers 0, 3 and -5 respectively on the number line. Points Q, R and S are between O and P such that OQ = QR = RS = SP.
What are the rational numbers represented by the points Q, R and S. Next choose a point T between Z and O so that ZT = TO. Which rational number does T represent?
Answer:
Given:
Points O, P, and Z represent the numbers 0, 3, and -5 respectively on the number line.
Points Q, R, and S are between O and P such that OQ = QR = RS = SP.
Point T is between Z and O such that ZT = TO.
To Find:
The rational numbers represented by points Q, R, and S.
The rational number represented by point T.
Solution:
Part 1: Finding the numbers represented by Q, R, and S.
The points O and P represent the numbers 0 and 3 respectively.
The segment OP is divided into 4 equal parts by the points Q, R, and S.
The length of the segment OP is the difference between the values represented by P and O:
Length of OP = $3 - 0 = 3$ units.
Since the segment OP is divided into 4 equal parts, the length of each part (OQ, QR, RS, SP) is $\frac{1}{4}$ of the total length.
Length of each part = $\frac{3}{4}$ units.
Point Q is at a distance of $\frac{3}{4}$ from O (which is at 0). So, the number represented by Q is:
Value of Q = $0 + \frac{3}{4} = \frac{3}{4}$
Point R is at a distance of 2 parts from O. So, the number represented by R is:
Value of R = $0 + 2 \times \frac{3}{4} = 2 \times \frac{3}{4} = \frac{6}{4} = \frac{3}{2}$
Point S is at a distance of 3 parts from O. So, the number represented by S is:
Value of S = $0 + 3 \times \frac{3}{4} = 3 \times \frac{3}{4} = \frac{9}{4}$
The rational numbers represented by points Q, R, and S are $\frac{3}{4}$, $\frac{3}{2}$, and $\frac{9}{4}$ respectively.
Part 2: Finding the number represented by T.
The points Z and O represent the numbers -5 and 0 respectively.
Point T is between Z and O such that ZT = TO. This means T is the midpoint of the segment ZO.
The value represented by the midpoint of a segment on a number line is the average of the values of the endpoints.
Value of T = $\frac{\text{Value of Z} + \text{Value of O}}{2}$
Value of T = $\frac{-5 + 0}{2}$
Value of T = $\frac{-5}{2}$
The rational number represented by point T is $\frac{-5}{2}$.
The rational numbers represented by the points Q, R and S are $\frac{3}{4}$, $\frac{3}{2}$ and $\frac{9}{4}$.
The rational number represented by point T is $\frac{-5}{2}$.
Example 11: A farmer has a field of area $49\frac{4}{5}$ ha. He wants to divide it equally among his one son and two daughters. Find the area of each one’s share.
(ha means hectare; 1 hectare = 10,000 m2)
Answer:
Given:
Total area of the farmer's field = $49\frac{4}{5}$ ha.
The field is to be divided equally among his one son and two daughters.
To Find:
The area of each one's share.
Solution:
The total area of the field is given as a mixed number: $49\frac{4}{5}$ ha.
First, convert the mixed number to an improper fraction:
$49\frac{4}{5} = \frac{(49 \times 5) + 4}{5}$
$= \frac{245 + 4}{5} = \frac{249}{5}$ ha.
The total area of the field is $\frac{249}{5}$ ha.
The farmer wants to divide the field equally among his one son and two daughters. This means the field is divided into a total of $1 \text{ (son)} + 2 \text{ (daughters)} = 3$ equal shares.
To find the area of each one's share, we need to divide the total area by the number of shares:
Area of each share = $\frac{\text{Total area}}{\text{Number of shares}}$
Area of each share = $\frac{\frac{249}{5}}{3}$
Dividing by 3 is the same as multiplying by the reciprocal of 3, which is $\frac{1}{3}$.
Area of each share = $\frac{249}{5} \times \frac{1}{3}$
Multiply the numerators and the denominators:
Area of each share = $\frac{249 \times 1}{5 \times 3} = \frac{249}{15}$
We can simplify the fraction $\frac{249}{15}$. Both 249 and 15 are divisible by 3.
$\frac{249}{15} = \frac{\cancel{249}^{83}}{\cancel{15}_{5}} = \frac{83}{5}$
The area of each share is $\frac{83}{5}$ ha.
We can also express this as a mixed number:
$\frac{83}{5} = 16\frac{3}{5}$
This means $83 \div 5$ gives a quotient of 16 and a remainder of 3.
The area of each one's share is $\frac{83}{5}$ ha or $16\frac{3}{5}$ ha.
Example 12: Let a, b, c be the three rational numbers where a = $\frac{3}{2}$ , b = $\frac{4}{5}$ , and c = $-\frac{5}{6}$
Verify:
(i) a + (b + c) = (a + b) + c (Associative property of addition)
(ii) a × (b × c) = (a × b) × c (Associative property of multiplication)
Answer:
Given:
$a = \frac{3}{2}$, $b = \frac{4}{5}$, $c = -\frac{5}{6}$.
To Verify:
(i) $a + (b + c) = (a + b) + c$
(ii) $a \times (b \times c) = (a \times b) \times c$
Solution:
(i) Verification of Associative property of addition:
Calculate LHS: $a + (b + c)$
LHS = $\frac{3}{2} + \left(\frac{4}{5} + (-\frac{5}{6})\right)$
LHS = $\frac{3}{2} + \left(\frac{24-25}{30}\right)$
LHS = $\frac{3}{2} + \frac{-1}{30}$
LHS = $\frac{45-1}{30} = \frac{44}{30} = \frac{22}{15}$
Calculate RHS: $(a + b) + c$
RHS = $\left(\frac{3}{2} + \frac{4}{5}\right) + (-\frac{5}{6})$
RHS = $\left(\frac{15+8}{10}\right) + (-\frac{5}{6})$
RHS = $\frac{23}{10} - \frac{5}{6}$
RHS = $\frac{69-25}{30} = \frac{44}{30} = \frac{22}{15}$
Since LHS = RHS = $\frac{22}{15}$, the associative property of addition is verified.
(ii) Verification of Associative property of multiplication:
Calculate LHS: $a \times (b \times c)$
LHS = $\frac{3}{2} \times \left(\frac{4}{5} \times (-\frac{5}{6})\right)$
LHS = $\frac{3}{2} \times \left(\frac{4 \times -5}{5 \times 6}\right)$
LHS = $\frac{3}{2} \times \left(\frac{-20}{30}\right) = \frac{3}{2} \times \frac{-2}{3}$
LHS = $\frac{3 \times -2}{2 \times 3} = \frac{-6}{6} = -1$
Calculate RHS: $(a \times b) \times c$
RHS = $\left(\frac{3}{2} \times \frac{4}{5}\right) \times (-\frac{5}{6})$
RHS = $\left(\frac{3 \times 4}{2 \times 5}\right) \times (-\frac{5}{6})$
RHS = $\frac{12}{10} \times (-\frac{5}{6}) = \frac{6}{5} \times (-\frac{5}{6})$
RHS = $\frac{6 \times -5}{5 \times 6} = \frac{-30}{30} = -1$
Since LHS = RHS = -1, the associative property of multiplication is verified.
Both properties are verified for the given rational numbers.
Example 13: Solve the following questions and write your observations.
(i) $\frac{5}{3}$ + 0 = ?
(ii) $\frac{-2}{5}$ + 0 = ?
(iii) $\frac{3}{7}$ + 0 = ?
(iv) $\frac{2}{3}$ × 1 = ?
(v) $\frac{-6}{7}$ × 1 = ?
(vi) $\frac{9}{8}$ × 1 = ?
Answer:
Given:
The given expressions involving addition with 0 and multiplication with 1.
To Solve and Observe:
Evaluate each expression and write observations.
Solution:
(i) $\frac{5}{3} + 0$
$\frac{5}{3} + 0 = \frac{5}{3}$
(ii) $\frac{-2}{5} + 0$
$\frac{-2}{5} + 0 = \frac{-2}{5}$
(iii) $\frac{3}{7} + 0$
$\frac{3}{7} + 0 = \frac{3}{7}$
(iv) $\frac{2}{3} \times 1$
$\frac{2}{3} \times 1 = \frac{2}{3}$
(v) $\frac{-6}{7} \times 1$
$\frac{-6}{7} \times 1 = \frac{-6}{7}$
(vi) $\frac{9}{8} \times 1$
$\frac{9}{8} \times 1 = \frac{9}{8}$
Observations:
From the results of (i), (ii), and (iii), we observe that when 0 is added to any rational number, the result is the rational number itself. This shows that 0 is the additive identity for rational numbers.
From the results of (iv), (v), and (vi), we observe that when any rational number is multiplied by 1, the result is the rational number itself. This shows that 1 is the multiplicative identity for rational numbers.
Example 14: Write any 5 rational numbers between $\frac{-5}{6}$ and $\frac{7}{8}$
Answer:
Given:
Two rational numbers are $\frac{-5}{6}$ and $\frac{7}{8}$.
To Find:
Any 5 rational numbers between $\frac{-5}{6}$ and $\frac{7}{8}$.
Solution:
To find rational numbers between two given rational numbers, we express them with a common denominator.
The denominators are 6 and 8.
We find the Least Common Multiple (LCM) of 6 and 8.
$\begin{array}{c|cc} 2 & 6 \;, & 8 \\ \hline 3 & 3 \; , & 4 \\ \hline 4 & 1 \; , & 4 \\ \hline & 1 \; , & 1 \end{array}$
LCM of 6 and 8 = $2 \times 3 \times 4 = 24$.
Now, express both fractions with a denominator of 24:
$\frac{-5}{6} = \frac{-5 \times 4}{6 \times 4} = \frac{-20}{24}$
$\frac{7}{8} = \frac{7 \times 3}{8 \times 3} = \frac{21}{24}$
Now we need to find 5 rational numbers between $\frac{-20}{24}$ and $\frac{21}{24}$.
We can choose any 5 integers between -20 and 21 and use them as numerators with the denominator 24.
The integers between -20 and 21 are -19, -18, -17, ..., 0, 1, 2, ..., 20.
We can pick any 5 of these integers. For example, let's pick -10, -5, 0, 5, 10.
The corresponding rational numbers are:
$\frac{-10}{24}, \frac{-5}{24}, \frac{0}{24}, \frac{5}{24}, \frac{10}{24}$
We can simplify these fractions (optional, but good practice):
$\frac{-10}{24} = \frac{\cancel{-10}^{-5}}{\cancel{24}_{12}} = \frac{-5}{12}$
$\frac{-5}{24}$
$\frac{0}{24} = 0$
$\frac{5}{24}$
$\frac{10}{24} = \frac{\cancel{10}^{5}}{\cancel{24}_{12}} = \frac{5}{12}$
These 5 rational numbers are indeed between $\frac{-20}{24}$ and $\frac{21}{24}$.
Any 5 rational numbers between $\frac{-5}{6}$ and $\frac{7}{8}$ are $\frac{-10}{24}$, $\frac{-5}{24}$, $0$, $\frac{5}{24}$, $\frac{10}{24}$.
(Note: There are infinitely many rational numbers between any two distinct rational numbers, so other sets of 5 numbers are also possible.)
Example 15: Identify the rational number which is different from the other three:
$\frac{2}{3}$ , $\frac{-4}{5}$ , $\frac{1}{2}$ , $\frac{1}{3}$ . Explain your reasoning
Answer:
Given:
The list of rational numbers: $\frac{2}{3}$, $\frac{-4}{5}$, $\frac{1}{2}$, $\frac{1}{3}$.
To Identify and Explain:
Identify the rational number that is different from the others and explain the reasoning.
Solution:
Let's look at the given rational numbers:
$\frac{2}{3}$
$\frac{-4}{5}$
$\frac{1}{2}$
$\frac{1}{3}$
We can observe the sign of each rational number.
The rational number $\frac{2}{3}$ is positive.
The rational number $\frac{-4}{5}$ is negative.
The rational number $\frac{1}{2}$ is positive.
The rational number $\frac{1}{3}$ is positive.
Three of the given rational numbers ($\frac{2}{3}$, $\frac{1}{2}$, and $\frac{1}{3}$) are positive rational numbers.
The rational number $\frac{-4}{5}$ is a negative rational number.
Therefore, the rational number $\frac{-4}{5}$ is different from the other three because it is the only negative number in the list.
The rational number which is different from the other three is $\frac{-4}{5}$.
Reasoning: The numbers $\frac{2}{3}$, $\frac{1}{2}$, and $\frac{1}{3}$ are all positive rational numbers, while $\frac{-4}{5}$ is a negative rational number. Since the sign of the number is a distinguishing property, $\frac{-4}{5}$ stands out as being different from the rest.
Example 16: Problem Solving Strategies
Problem: The product of two rational numbers is –7. If one of the number is –10, find the other.
Answer:
Given:
Product of two rational numbers $= -7$
One of the numbers $= -10$
To Find:
The other rational number.
Solution:
Let the other rational number be $x$.
According to the given problem, the product of the two rational numbers is $-7$.
So, we can write the equation:
$(-10) \times x = -7$
To find the value of $x$, we divide both sides of the equation by $-10$.
$x = \frac{-7}{-10}$
Simplifying the fraction, we get:
$x = \frac{7}{10}$
Thus, the other rational number is $\frac{7}{10}$.
Exercise
Question 1 to 25 (Multiple Choice Questions)
In questions 1 to 25, there are four options out of which one is correct. Choose the correct answer.
Question 1. A number which can be expressed as $\frac{p}{q}$ where p and q are integers and q ≠ 0 is
(a) natural number.
(b) whole number.
(c) integer.
(d) rational number.
Answer:
The correct answer is (d) rational number.
A rational number is defined as any number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
Question 2. A number of the form $\frac{p}{q}$ is said to be a rational number if
(a) p and q are integers.
(b) p and q are integers and q ≠ 0
(c) p and q are integers and p ≠ 0
(d) p and q are integers and p ≠ 0 also q ≠ 0.
Answer:
The correct answer is (b) p and q are integers and q ≠ 0.
A rational number is defined as any number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and the denominator $q$ is not equal to zero ($q \neq 0$).
Let's examine the options:
(a) "p and q are integers." This condition is necessary, but not sufficient. If $q=0$, the expression $\frac{p}{q}$ is undefined. For example, $\frac{5}{0}$ is not a number, and thus not a rational number, even though $p=5$ and $q=0$ are integers.
(b) "p and q are integers and q ≠ 0". This is the precise definition of a rational number. Both the numerator $p$ and the denominator $q$ must be integers, and the denominator $q$ must not be zero to avoid division by zero.
(c) "p and q are integers and p ≠ 0". This is incorrect. The numerator $p$ can be zero. For example, $\frac{0}{5} = 0$. Here, $p=0$ and $q=5$. Both are integers, and $q \neq 0$. The number $0$ is a rational number because it can be expressed as $\frac{0}{q}$ for any non-zero integer $q$.
(d) "p and q are integers and p ≠ 0 also q ≠ 0". This is incorrect for the same reason as (c) - the numerator $p$ is allowed to be zero in a rational number.
Therefore, the essential conditions for a number of the form $\frac{p}{q}$ to be a rational number are that $p$ and $q$ must be integers, and $q$ must not be zero.
Question 3. The numerical expression $\frac{3}{8}$ + $\frac{(-5)}{7}$ = $\frac{-19}{56}$ shows that
(a) rational numbers are closed under addition.
(b) rational numbers are not closed under addition.
(c) rational numbers are closed under multiplication.
(d) addition of rational numbers is not commutative.
Answer:
The correct answer is (a) rational numbers are closed under addition.
The closure property under addition states that for any two rational numbers $a$ and $b$, their sum $a+b$ is also a rational number.
In the given expression, $\frac{3}{8}$ is a rational number and $\frac{(-5)}{7}$ is a rational number.
Their sum is $\frac{-19}{56}$, which is also a rational number (since $-19$ and $56$ are integers and $56 \neq 0$).
This example illustrates that the set of rational numbers is closed under the operation of addition.
Question 4. Which of the following is not true?
(a) rational numbers are closed under addition.
(b) rational numbers are closed under subtraction.
(c) rational numbers are closed under multiplication.
(d) rational numbers are closed under division.
Answer:
The correct answer is (d) rational numbers are closed under division.
Let's examine the closure property for each operation on rational numbers:
(a) Addition: For any two rational numbers $\frac{a}{b}$ and $\frac{c}{d}$ (where $b \neq 0, d \neq 0$), their sum is $\frac{a}{b} + \frac{c}{d} = \frac{ad+bc}{bd}$. Since $a, b, c, d$ are integers and $b \neq 0, d \neq 0$, it follows that $ad+bc$ is an integer and $bd$ is a non-zero integer. Therefore, $\frac{ad+bc}{bd}$ is a rational number. Rational numbers are closed under addition.
(b) Subtraction: For any two rational numbers $\frac{a}{b}$ and $\frac{c}{d}$ (where $b \neq 0, d \neq 0$), their difference is $\frac{a}{b} - \frac{c}{d} = \frac{ad-bc}{bd}$. Since $a, b, c, d$ are integers and $b \neq 0, d \neq 0$, it follows that $ad-bc$ is an integer and $bd$ is a non-zero integer. Therefore, $\frac{ad-bc}{bd}$ is a rational number. Rational numbers are closed under subtraction.
(c) Multiplication: For any two rational numbers $\frac{a}{b}$ and $\frac{c}{d}$ (where $b \neq 0, d \neq 0$), their product is $\frac{a}{b} \times \frac{c}{d} = \frac{ac}{bd}$. Since $a, b, c, d$ are integers and $b \neq 0, d \neq 0$, it follows that $ac$ is an integer and $bd$ is a non-zero integer. Therefore, $\frac{ac}{bd}$ is a rational number. Rational numbers are closed under multiplication.
(d) Division: For any two rational numbers $\frac{a}{b}$ and $\frac{c}{d}$ (where $b \neq 0, d \neq 0$), their quotient is $\frac{a}{b} \div \frac{c}{d}$. Division is only defined when the divisor is non-zero, i.e., $\frac{c}{d} \neq 0$, which means $c \neq 0$. If $\frac{c}{d} \neq 0$, then $\frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \times \frac{d}{c} = \frac{ad}{bc}$. Since $a, b, c, d$ are integers and $b \neq 0, d \neq 0, c \neq 0$, it follows that $ad$ is an integer and $bc$ is a non-zero integer. So $\frac{ad}{bc}$ is a rational number.
However, the closure property for division states that the set is closed if the result of dividing any two elements in the set (where the divisor is non-zero) is also in the set. While this is true for non-zero divisors, the statement "rational numbers are closed under division" is usually understood to mean that for *any* two rational numbers $a$ and $b$, $a \div b$ is rational, provided $b \neq 0$. A simpler way to view why it's often stated that rational numbers are *not* closed under division is because the operation is not defined for all pairs of rational numbers (specifically, when the second number is $0$, which is a rational number). If we consider the set of rational numbers excluding zero ($\mathbb{Q} \setminus \{0\}$), then that set is closed under division. But the set of all rational numbers ($\mathbb{Q}$) is not closed under division because division by the rational number $0$ is undefined.
Therefore, the statement that is not true is that rational numbers are closed under division, because division by the rational number 0 is not possible within the set of rational numbers.
Question 5. $-\frac{3}{8}$ + $\frac{1}{7}$ = $\frac{1}{7}$ + $\left( \frac{-3}{8} \right)$ is an example to show that
(a) addition of rational numbers is commutative.
(b) rational numbers are closed under addition.
(c) addition of rational number is associative.
(d) rational numbers are distributive under addition.
Answer:
The correct answer is (a) addition of rational numbers is commutative.
The given expression is $-\frac{3}{8}$ + $\frac{1}{7}$ = $\frac{1}{7}$ + $\left( \frac{-3}{8} \right)$.
This expression shows that the order of the operands in an addition operation does not affect the result.
This property, $a + b = b + a$, is known as the commutative property of addition.
Since $-\frac{3}{8}$ and $\frac{1}{7}$ are rational numbers, this example demonstrates the commutative property for the addition of rational numbers.
Question 6. Which of the following expressions shows that rational numbers are associative under multiplication.
(a) $\frac{2}{3}$ × $\left( \frac{-6}{7} \times \frac{3}{5} \right)$ = $\left( \frac{2}{3} \times \frac{-6}{7} \right)$ × $\frac{3}{5}$
(b) $\frac{2}{3}$ × $\left( \frac{-6}{7} \times \frac{3}{5} \right)$ = $\frac{2}{3}$ × $\left( \frac{3}{5} \times \frac{-6}{7} \right)$
(c) $\frac{2}{3}$ × $\left( \frac{-6}{7} \times \frac{3}{5} \right)$ = $\left( \frac{3}{5} \times \frac{2}{3} \right)$ × $\frac{-6}{7}$
(d) $\left( \frac{2}{3} \times \frac{-6}{7} \right)$ × $\frac{3}{5}$ = $\left( \frac{-6}{7} \times \frac{2}{3} \right)$ ) × $\frac{3}{5}$
Answer:
The correct answer is (a) $\frac{2}{3}$ × $\left( \frac{-6}{7} \times \frac{3}{5} \right)$ = $\left( \frac{2}{3} \times \frac{-6}{7} \right)$ × $\frac{3}{5}$.
The associative property of multiplication states that for any three rational numbers $a$, $b$, and $c$, the grouping of the numbers in a multiplication does not affect the result. Mathematically, this is expressed as:
$(a \times b) \times c = a \times (b \times c)$
Looking at the given options:
(a) $\frac{2}{3} \times \left( \frac{-6}{7} \times \frac{3}{5} \right)$ = $\left( \frac{2}{3} \times \frac{-6}{7} \right)$ × $\frac{3}{5}$ matches the form $a \times (b \times c) = (a \times b) \times c$, where $a = \frac{2}{3}$, $b = \frac{-6}{7}$, and $c = \frac{3}{5}$. This expression directly demonstrates the associative property of multiplication.
(b) $\frac{2}{3} \times \left( \frac{-6}{7} \times \frac{3}{5} \right)$ = $\frac{2}{3} \times \left( \frac{3}{5} \times \frac{-6}{7} \right)$ shows the commutative property of multiplication ($b \times c = c \times b$) inside the parenthesis.
(c) $\frac{2}{3}$ × $\left( \frac{-6}{7} \times \frac{3}{5} \right)$ = $\left( \frac{3}{5} \times \frac{2}{3} \right)$ × $\frac{-6}{7}$ involves both commutative and associative properties, but it is not the standard representation of associativity.
(d) $\left( \frac{2}{3} \times \frac{-6}{7} \right)$ × $\frac{3}{5}$ = $\left( \frac{-6}{7} \times \frac{2}{3} \right)$ × $\frac{3}{5}$ shows the commutative property of multiplication ($a \times b = b \times a$) inside the left parenthesis.
Therefore, option (a) is the expression that specifically shows that rational numbers are associative under multiplication.
Question 7. Zero (0) is
(a) the identity for addition of rational numbers.
(b) the identity for subtraction of rational numbers.
(c) the identity for multiplication of rational numbers.
(d) the identity for division of rational numbers.
Answer:
The correct answer is (a) the identity for addition of rational numbers.
An identity element for an operation is an element which, when combined with any other element from the set using that operation, leaves the other element unchanged.
For addition of rational numbers, the identity element $e$ must satisfy $a + e = a$ and $e + a = a$ for any rational number $a$.
Let's check if $0$ satisfies this for addition:
$a + 0 = a$
$0 + a = a$
This is true for all rational numbers $a$. Therefore, $0$ is the additive identity for rational numbers.
For subtraction, $a - 0 = a$, but $0 - a = -a$. Since $-a$ is not generally equal to $a$, $0$ is not the identity for subtraction.
For multiplication, $a \times 0 = 0$ and $0 \times a = 0$. The multiplicative identity is $1$, because $a \times 1 = a$ and $1 \times a = a$. So $0$ is not the identity for multiplication.
For division, $a \div 0$ is undefined, so $0$ cannot be the identity for division.
Question 8. One (1) is
(a) the identity for addition of rational numbers.
(b) the identity for subtraction of rational numbers.
(c) the identity for multiplication of rational numbers.
(d) the identity for division of rational numbers.
Answer:
The correct answer is (c) the identity for multiplication of rational numbers.
An identity element for an operation is an element which, when combined with any other element from the set using that operation, leaves the other element unchanged.
For multiplication of rational numbers, the identity element $e$ must satisfy $a \times e = a$ and $e \times a = a$ for any rational number $a$.
Let's check if $1$ satisfies this for multiplication:
$a \times 1 = a$
$1 \times a = a$
This is true for all rational numbers $a$. Therefore, $1$ is the multiplicative identity for rational numbers.
For addition, the identity element is $0$ because $a + 0 = a$. $a + 1$ is not equal to $a$ in general.
For subtraction, $a - 1 \neq a$ (unless $a=0$), and $1 - a \neq a$ (unless $a=1/2$). So $1$ is not the identity for subtraction.
For division, $a \div 1 = a$, but $1 \div a = \frac{1}{a}$. For $1$ to be the identity, we would need $a \div 1 = a$ and $1 \div a = a$. The second part $1/a = a$ is only true when $a^2 = 1$, i.e., $a=1$ or $a=-1$. Since this is not true for all rational numbers $a$, $1$ is not the identity for division (though it is a right identity).
Question 9. The additive inverse of $\frac{-7}{19}$ is
(a) $\frac{-7}{19}$
(b) $\frac{7}{19}$
(c) $\frac{19}{7}$
(d) $\frac{-19}{7}$
Answer:
The correct answer is (b) $\frac{7}{19}$.
The additive inverse of a rational number $a$ is the rational number $-a$ such that their sum is the additive identity, $0$. That is, $a + (-a) = 0$.
Let the given rational number be $a = \frac{-7}{19}$.
Its additive inverse is $-a = -(\frac{-7}{19}) = \frac{7}{19}$.
We can verify this by adding the number and its additive inverse:
$\frac{-7}{19} + \frac{7}{19} = \frac{-7+7}{19} = \frac{0}{19} = 0$.
Question 10. Multiplicative inverse of a negative rational number is
(a) a positive rational number.
(b) a negative rational number.
(c) 0
(d) 1
Answer:
The correct answer is (b) a negative rational number.
The multiplicative inverse (or reciprocal) of a non-zero rational number $a$ is the rational number $\frac{1}{a}$ such that their product is the multiplicative identity, $1$. That is, $a \times \frac{1}{a} = 1$.
Let the negative rational number be $x$. Since $x$ is a rational number, we can write it as $x = \frac{p}{q}$, where $p$ and $q$ are integers, $q \neq 0$. Since $x$ is negative, $\frac{p}{q} < 0$. This means that $p$ and $q$ must have opposite signs (one is positive and the other is negative).
The multiplicative inverse of $x = \frac{p}{q}$ is $\frac{1}{x} = \frac{q}{p}$.
Since $p$ and $q$ have opposite signs, their quotient $\frac{q}{p}$ will also be negative.
For example, consider the negative rational number $\frac{-3}{5}$. Its multiplicative inverse is $\frac{5}{-3}$, which is equal to $\frac{-5}{3}$. Both $\frac{-3}{5}$ and $\frac{-5}{3}$ are negative rational numbers.
Another example, consider the negative rational number $\frac{2}{-7}$. Its multiplicative inverse is $\frac{-7}{2}$. Both $\frac{2}{-7}$ and $\frac{-7}{2}$ are negative rational numbers.
Therefore, the multiplicative inverse of a negative rational number is always a negative rational number.
Question 11. If x + 0 = 0 + x = x, which is rational number, then 0 is called
(a) identity for addition of rational numbers.
(b) additive inverse of x.
(c) multiplicative inverse of x.
(d) reciprocal of x.
Answer:
The correct answer is (a) identity for addition of rational numbers.
The property stated, $x + 0 = 0 + x = x$ for any rational number $x$, is the definition of the identity element for the operation of addition.
An identity element $e$ for an operation $*$ on a set $S$ is an element such that for every element $a$ in $S$, $a * e = e * a = a$.
In this case, the set is rational numbers ($\mathbb{Q}$), the operation is addition ($+$), and the element $0$ satisfies the property $x + 0 = 0 + x = x$ for any rational number $x$.
Therefore, $0$ is the additive identity for rational numbers.
Question 12. To get the product 1, we should multiply $\frac{8}{21}$ by
(a) $\frac{8}{21}$
(b) $\frac{-8}{21}$
(c) $\frac{21}{8}$
(d) $\frac{-21}{8}$
Answer:
The correct answer is (c) $\frac{21}{8}$.
To get the product 1 when multiplying by a non-zero number, we must multiply by its multiplicative inverse (or reciprocal).
The multiplicative inverse of a non-zero rational number $\frac{p}{q}$ is $\frac{q}{p}$, such that $\frac{p}{q} \times \frac{q}{p} = 1$.
The given number is $\frac{8}{21}$.
Its multiplicative inverse is the reciprocal, which is found by swapping the numerator and the denominator.
The reciprocal of $\frac{8}{21}$ is $\frac{21}{8}$.
Let's check the multiplication:
$\frac{8}{21} \times \frac{21}{8} = \frac{\cancel{8}^{1}}{\cancel{21}^{1}} \times \frac{\cancel{21}^{1}}{\cancel{8}^{1}} = \frac{1 \times 1}{1 \times 1} = 1$
So, multiplying $\frac{8}{21}$ by $\frac{21}{8}$ gives the product 1.
Question 13. – (–x) is same as
(a) – x
(b) x
(c) $\frac{1}{x}$
(d) $\frac{-1}{x}$
Answer:
The correct answer is (b) x.
The expression $– (–x)$ means the additive inverse of $(-x)$.
The additive inverse of a number is the number that, when added to the original number, results in $0$.
For any rational number $x$, its additive inverse is $-x$ because $x + (-x) = 0$.
Similarly, for the rational number $-x$, its additive inverse is $–(–x)$ because $(-x) + (–(–x)) = 0$.
Since the additive inverse of $-x$ is $x$ (as $(-x) + x = 0$), it must be that $–(–x) = x$.
This property is known as the double negation property.
So, $– (–x) = x$.
Question 14. The multiplicative inverse of $-1\frac{1}{7}$ is
(a) $\frac{8}{7}$
(b) $\frac{-8}{7}$
(c) $\frac{7}{8}$
(d) $\frac{7}{-8}$
Answer:
The correct answer is (d) $\frac{7}{-8}$.
First, convert the mixed number $-1\frac{1}{7}$ into an improper fraction.
$-1\frac{1}{7} = -(1 + \frac{1}{7})$
$-1\frac{1}{7} = -(\frac{7 \times 1 + 1}{7})$
$-1\frac{1}{7} = -\frac{8}{7}$
The multiplicative inverse of a non-zero rational number $\frac{p}{q}$ is $\frac{q}{p}$, such that their product is $1$.
The given number is $\frac{-8}{7}$.
Its multiplicative inverse is the reciprocal, which is obtained by inverting the fraction:
Multiplicative inverse of $\frac{-8}{7}$ is $\frac{7}{-8}$.
We can verify this by multiplying the number and its inverse:
$\frac{-8}{7} \times \frac{7}{-8} = \frac{\cancel{-8}^{-1}}{\cancel{7}^{1}} \times \frac{\cancel{7}^{1}}{\cancel{-8}^{-1}} = \frac{-1 \times 1}{1 \times -1} = \frac{-1}{-1} = 1$
Thus, the multiplicative inverse of $-1\frac{1}{7}$ is $\frac{7}{-8}$.
Question 15. If x be any rational number then x + 0 is equal to
(a) x
(b) 0
(c) – x
(d) Not defined
Answer:
The correct answer is (a) x.
The number $0$ is the additive identity for rational numbers.
The property of the additive identity states that for any rational number $x$, the sum of $x$ and $0$ is equal to $x$.
Mathematically, this is expressed as:
$x + 0 = x$
and also $0 + x = x$.
Therefore, for any rational number $x$, $x + 0$ is equal to $x$.
Question 16. The reciprocal of 1 is
(a) 1
(b) –1
(c) 0
(d) Not defined
Answer:
The correct answer is (a) 1.
The reciprocal of a non-zero number is its multiplicative inverse. If a number is $a$, its reciprocal is $\frac{1}{a}$.
We need to find the reciprocal of $1$.
Using the definition, the reciprocal of $1$ is $\frac{1}{1}$.
$\frac{1}{1} = 1$
Alternatively, the reciprocal of a number is the number that, when multiplied by the original number, gives a product of 1.
Let the reciprocal of 1 be $y$. Then, $1 \times y = 1$.
The only number that satisfies this equation is $y=1$.
Thus, the reciprocal of 1 is 1.
Question 17. The reciprocal of –1 is
(a) 1
(b) –1
(c) 0
(d) Not defined
Answer:
The correct answer is (b) –1.
The reciprocal of a non-zero number is its multiplicative inverse. If a number is $a$, its reciprocal is $\frac{1}{a}$.
We need to find the reciprocal of $-1$.
Using the definition, the reciprocal of $-1$ is $\frac{1}{-1}$.
$\frac{1}{-1} = -1$
Alternatively, the reciprocal of a number is the number that, when multiplied by the original number, gives a product of 1.
Let the reciprocal of $-1$ be $y$. Then, $-1 \times y = 1$.
To find $y$, we divide both sides by $-1$:
$y = \frac{1}{-1}$
$y = -1$
Thus, the reciprocal of $-1$ is $-1$.
Question 18. The reciprocal of 0 is
(a) 1
(b) –1
(c) 0
(d) Not defined
Answer:
The correct answer is (d) Not defined.
The reciprocal of a number $a$ is its multiplicative inverse, denoted as $\frac{1}{a}$.
The reciprocal is defined only for non-zero numbers.
Division by zero is an undefined operation in mathematics.
To find the reciprocal of 0, we would attempt to calculate $\frac{1}{0}$.
Since division by 0 is not allowed, the expression $\frac{1}{0}$ is undefined.
Therefore, the reciprocal of 0 does not exist or is not defined.
Question 19. The reciprocal of any rational number $\frac{p}{q}$ , where p and q are integers and q ≠ 0, is
(a) $\frac{p}{q}$
(b) 1
(c) 0
(d) $\frac{q}{p}$
Answer:
The correct answer is (d) $\frac{q}{p}$.
The reciprocal of a non-zero number is its multiplicative inverse.
For a rational number $\frac{p}{q}$, its multiplicative inverse is a number $y$ such that $\frac{p}{q} \times y = 1$.
If $p \neq 0$, the multiplicative inverse is $\frac{q}{p}$, provided $q \neq 0$.
Then $\frac{p}{q} \times \frac{q}{p} = \frac{pq}{qp} = 1$ (assuming $p \neq 0$ and $q \neq 0$).
The question states that $\frac{p}{q}$ is a rational number where $p$ and $q$ are integers and $q \neq 0$.
However, for the reciprocal $\frac{q}{p}$ to be defined as a rational number, we also need the denominator $p$ to be non-zero.
If $p=0$, the rational number is $\frac{0}{q} = 0$ (since $q \neq 0$). The reciprocal of $0$ is undefined, as discussed in Question 18.
Assuming the question implies a non-zero rational number $\frac{p}{q}$ (i.e., $p \neq 0$ and $q \neq 0$), then the reciprocal is $\frac{q}{p}$.
Option (d) is $\frac{q}{p}$. This is the correct form of the reciprocal, assuming $p \neq 0$.
It's worth noting that the question phrasing "any rational number $\frac{p}{q}$" might implicitly exclude the case $p=0$, since the reciprocal of $0$ isn't a rational number itself (it's undefined).
Question 20. If y be the reciprocal of rational number x, then the reciprocal of y will be
(a) x
(b) y
(c) $\frac{x}{y}$
(d) $\frac{y}{x}$
Answer:
The correct answer is (a) x.
We are given that $y$ is the reciprocal of the rational number $x$.
By the definition of a reciprocal, this means that the product of $x$ and $y$ is equal to the multiplicative identity, which is $1$.
So, we have the relationship:
$x \times y = 1$
This implies that $x$ must be a non-zero rational number for its reciprocal $y$ to exist, and $y$ must also be a non-zero rational number.
We are asked to find the reciprocal of $y$. Let the reciprocal of $y$ be $z$.
By the definition of a reciprocal, the product of $y$ and $z$ must be $1$.
$y \times z = 1$
We can find $z$ by dividing both sides of this equation by $y$ (since $y \neq 0$):
$z = \frac{1}{y}$
From the initial relationship $x \times y = 1$, we can also express $x$ in terms of $y$ by dividing both sides by $y$:
$x = \frac{1}{y}$
Comparing the expressions for $z$ and $x$, we see that $z = x$.
Therefore, the reciprocal of $y$ is $x$.
Alternatively, if $y$ is the reciprocal of $x$, then $y = \frac{1}{x}$. The reciprocal of $y$ is $\frac{1}{y}$. Substituting $y=\frac{1}{x}$, we get:
Reciprocal of $y = \frac{1}{y} = \frac{1}{\left(\frac{1}{x}\right)}$
$\frac{1}{\left(\frac{1}{x}\right)} = 1 \div \frac{1}{x} = 1 \times \frac{x}{1} = x$
So, the reciprocal of $y$ is $x$.
Question 21. The reciprocal of $\frac{-3}{8} \times \left( \frac{-7}{13} \right)$ is
(a) $\frac{104}{21}$
(b) $\frac{-104}{21}$
(c) $\frac{21}{104}$
(d) $\frac{-21}{104}$
Answer:
The correct answer is (a) $\frac{104}{21}$.
First, we need to calculate the product of the two rational numbers:
$\frac{-3}{8} \times \left( \frac{-7}{13} \right) = \frac{(-3) \times (-7)}{8 \times 13}$
$\frac{(-3) \times (-7)}{8 \times 13} = \frac{21}{104}$
Now, we need to find the reciprocal of the result, which is $\frac{21}{104}$.
The reciprocal of a non-zero rational number $\frac{a}{b}$ is $\frac{b}{a}$.
So, the reciprocal of $\frac{21}{104}$ is $\frac{104}{21}$.
Question 22. Which of the following is an example of distributive property of multiplication over addition for rational numbers.
(a) $-\frac{1}{4}\times\left\{ \frac{2}{3}+\left( \frac{-4}{7} \right) \right\}=\left[ -\frac{1}{4}\times\frac{2}{3} \right]+\left[ -\frac{1}{4}\times\left( \frac{-4}{7} \right) \right]$
(b) $-\frac{1}{4}\times\left\{ \frac{2}{3}+\left( \frac{-4}{7} \right) \right\}=\left[ \frac{1}{4}\times\frac{2}{3} \right]-\left( \frac{-4}{7} \right)$
(c) $-\frac{1}{4}\times\left\{ \frac{2}{3}+\left( \frac{-4}{7} \right) \right\}=\frac{2}{3}+\left( -\frac{1}{4} \right)\times\frac{-4}{7}$
(d) $-\frac{1}{4}\times\left\{ \frac{2}{3}+\left( \frac{-4}{7} \right) \right\}=\left\{ \frac{2}{3}+\left( \frac{-4}{7} \right) \right\}-\frac{1}{4}$
Answer:
The correct answer is (a) $-\frac{1}{4}\times\left\{ \frac{2}{3}+\left( \frac{-4}{7} \right) \right\}=\left[ -\frac{1}{4}\times\frac{2}{3} \right]+\left[ -\frac{1}{4}\times\left( \frac{-4}{7} \right) \right]$.
The distributive property of multiplication over addition states that for any three rational numbers $a$, $b$, and $c$, the product of $a$ and the sum of $b$ and $c$ is equal to the sum of the products of $a$ and $b$, and $a$ and $c$.
Mathematically, the distributive property is expressed as:
$a \times (b + c) = (a \times b) + (a \times c)$
Let's compare this form with the given options. In the question, we have the expression $-\frac{1}{4} \times \left\{ \frac{2}{3} + \left( \frac{-4}{7} \right) \right\}$.
Here, $a = -\frac{1}{4}$, $b = \frac{2}{3}$, and $c = \frac{-4}{7}$.
According to the distributive property, this should be equal to $(-\frac{1}{4} \times \frac{2}{3}) + (-\frac{1}{4} \times \frac{-4}{7})$.
Option (a) matches this form exactly:
$-\frac{1}{4}\times\left\{ \frac{2}{3}+\left( \frac{-4}{7} \right) \right\}=\left[ -\frac{1}{4}\times\frac{2}{3} \right]+\left[ -\frac{1}{4}\times\left( \frac{-4}{7} \right) \right]$
The other options do not follow the structure of the distributive property.
Question 23. Between two given rational numbers, we can find
(a) one and only one rational number.
(b) only two rational numbers.
(c) only ten rational numbers.
(d) infinitely many rational numbers.
Answer:
The correct answer is (d) infinitely many rational numbers.
The set of rational numbers is dense.
This means that between any two distinct rational numbers, there exists another rational number.
Let $a$ and $b$ be two distinct rational numbers such that $a < b$.
Consider their average, $\frac{a+b}{2}$.
If $a$ and $b$ are rational, then $a+b$ is rational, and $\frac{a+b}{2}$ is also rational.
Also, since $a < b$, adding $a$ to both sides gives $2a < a+b$, so $a < \frac{a+b}{2}$.
Similarly, adding $b$ to both sides of $a < b$ gives $a+b < 2b$, so $\frac{a+b}{2} < b$.
Thus, $\frac{a+b}{2}$ is a rational number strictly between $a$ and $b$.
Now we have three distinct rational numbers: $a$, $\frac{a+b}{2}$, and $b$. We can apply the same process again to find a rational number between $a$ and $\frac{a+b}{2}$, and another between $\frac{a+b}{2}$ and $b$.
For example, a rational number between $a$ and $\frac{a+b}{2}$ is $\frac{a + \frac{a+b}{2}}{2} = \frac{\frac{2a+a+b}{2}}{2} = \frac{3a+b}{4}$. This number is also rational and lies between $a$ and $b$.
Since we can always find a new rational number between any two existing distinct rational numbers, this process can be continued indefinitely.
Therefore, there are infinitely many rational numbers between any two given distinct rational numbers.
Question 24. $\frac{x \;+\; y}{2}$ is a rational number.
(a) Between x and y
(b) Less than x and y both.
(c) Greater than x and y both.
(d) Less than x but greater than y.
Answer:
The correct answer is (a) Between x and y.
If $x$ and $y$ are distinct rational numbers, let's assume without loss of generality that $x < y$.
Consider the expression $\frac{x+y}{2}$.
Since $x < y$, adding $x$ to both sides gives:
$x + x < y + x$
$2x < x+y$
Dividing by 2 (which is a positive number), the inequality is preserved:
$x < \frac{x+y}{2}$
Similarly, since $x < y$, adding $y$ to both sides gives:
$x + y < y + y$
$x+y < 2y$
Dividing by 2:
$\frac{x+y}{2} < y$
Combining the two inequalities, we have:
$x < \frac{x+y}{2} < y$
This shows that $\frac{x+y}{2}$ is a rational number that lies strictly between $x$ and $y$ (provided $x \neq y$). If $x=y$, then $\frac{x+y}{2} = \frac{x+x}{2} = x$, which is equal to both $x$ and $y$. However, the options refer to the position relative to potentially distinct numbers. The average method $\frac{x+y}{2}$ is a standard way to find a number located centrally between two numbers.
Question 25. Which of the following statements is always true?
(a) $\frac{x \;-\; y}{2}$ is a rational number between x and y.
(b) $\frac{x \;+\; y}{2}$ is a rational number between x and y.
(c) $\frac{x \;×\; y}{2}$ is a rational number between x and y.
(d) $\frac{x \;÷\; y}{2}$ is a rational number between x and y.
Answer:
The correct answer is (b) $\frac{x \;+\; y}{2}$ is a rational number between x and y.
Let $x$ and $y$ be any two rational numbers.
First, let's confirm that $\frac{x+y}{2}$ is always a rational number. Since rational numbers are closed under addition, $x+y$ is a rational number. Since $2$ is a non-zero rational number, and rational numbers are closed under division by a non-zero rational number, $\frac{x+y}{2}$ is also a rational number.
Now let's consider its position relative to $x$ and $y$.
If $x = y$, then $\frac{x+y}{2} = \frac{x+x}{2} = \frac{2x}{2} = x$. In this case, $\frac{x+y}{2}$ is equal to both $x$ and $y$, and lies in the interval $[min(x,y), max(x,y)] = [x,x]$.
If $x < y$, we have:
Adding $x$ to the inequality $x < y$:
$x + x < x + y$
$2x < x + y$
Dividing by $2$ (a positive number):
$x < \frac{x+y}{2}$
Adding $y$ to the inequality $x < y$:
$x + y < y + y$
$x + y < 2y$
Dividing by $2$:
$\frac{x+y}{2} < y$
Combining the two inequalities, we get $x < \frac{x+y}{2} < y$. This shows that $\frac{x+y}{2}$ is strictly between $x$ and $y$ when $x < y$.
If $y < x$, a similar argument would show $y < \frac{x+y}{2} < x$. This shows that $\frac{x+y}{2}$ is strictly between $y$ and $x$ when $y < x$.
So, in all cases ($x=y$ or $x \neq y$), $\frac{x+y}{2}$ is a rational number that lies in the closed interval $[min(x,y), max(x,y)]$. The statement "between x and y" in this context typically refers to this property.
Let's check the other options with counterexamples:
(a) $\frac{x-y}{2}$: If $x=1, y=2$, then $\frac{1-2}{2} = \frac{-1}{2}$. $\frac{-1}{2}$ is not between 1 and 2.
(c) $\frac{x \times y}{2}$: If $x=2, y=4$, then $\frac{2 \times 4}{2} = \frac{8}{2} = 4$. $4$ is not strictly between 2 and 4. If $x=1/2, y=1/4$, then $\frac{(1/2) \times (1/4)}{2} = \frac{1/8}{2} = \frac{1}{16}$. $\frac{1}{16}$ is not between $\frac{1}{4}$ and $\frac{1}{2}$ (since $\frac{1}{16} < \frac{1}{4}$).
(d) $\frac{x \div y}{2}$: This is not defined if $y=0$. Even if $y \neq 0$, e.g., $x=2, y=1$, then $\frac{2 \div 1}{2} = \frac{2}{2} = 1$. $1$ is not strictly between 2 and 1. If $x=1, y=2$, then $\frac{1 \div 2}{2} = \frac{1/2}{2} = 1/4$. $1/4$ is not between 1 and 2.
Therefore, the only statement that is always true for any rational numbers $x$ and $y$ (in the sense described) is that $\frac{x+y}{2}$ is a rational number between $x$ and $y$.
Question 26 to 47 (Fill in the Blanks)
In questions 26 to 47, fill in the blanks to make the statements true.
Question 26. The equivalent of $\frac{5}{7}$ , whose numerator is 45 is ___________.
Answer:
Let the equivalent fraction be $\frac{45}{q}$.
We are given that $\frac{5}{7} = \frac{45}{q}$.
To find the value of $q$, we can cross-multiply or observe the change in the numerator.
The numerator of the original fraction is 5, and the numerator of the equivalent fraction is 45.
The multiplication factor for the numerator is $\frac{45}{5} = 9$.
To get an equivalent fraction, we must multiply both the numerator and the denominator by the same non-zero number. In this case, the number is 9.
So, we multiply the denominator 7 by 9:
$q = 7 \times 9 = 63$
The equivalent fraction is $\frac{45}{63}$.
The equivalent of $\frac{5}{7}$ , whose numerator is 45 is $\frac{45}{63}$.
Question 27. The equivalent rational number of $\frac{7}{9}$ , whose denominator is 45 is ___________.
Answer:
Let the equivalent rational number be $\frac{p}{45}$.
We are given that the rational number $\frac{7}{9}$ is equivalent to $\frac{p}{45}$.
To find the equivalent fraction, we need to determine what factor the denominator 9 was multiplied by to get the denominator 45.
The factor is $45 \div 9 = 5$.
To maintain the equivalence, the numerator must be multiplied by the same factor.
$p = 7 \times 5 = 35$
So, the equivalent rational number is $\frac{35}{45}$.
The equivalent rational number of $\frac{7}{9}$ , whose denominator is 45 is $\frac{35}{45}$.
Question 28. Between the numbers $\frac{15}{20}$ and $\frac{35}{40}$ , the greater number is __________.
Answer:
To find the greater number between $\frac{15}{20}$ and $\frac{35}{40}$, we can simplify the fractions and then compare them using a common denominator.
Simplify the first fraction:
$\frac{15}{20} = \frac{3 \times 5}{4 \times 5} = \frac{3}{4}$
Simplify the second fraction:
$\frac{35}{40} = \frac{5 \times 7}{5 \times 8} = \frac{7}{8}$
Now we compare $\frac{3}{4}$ and $\frac{7}{8}$.
Find a common denominator for 4 and 8. The least common multiple is 8.
Convert $\frac{3}{4}$ to an equivalent fraction with denominator 8:
$\frac{3}{4} = \frac{3 \times 2}{4 \times 2} = \frac{6}{8}$
Now compare $\frac{6}{8}$ and $\frac{7}{8}$.
Since the denominators are the same, we compare the numerators.
$6 < 7$
Therefore, $\frac{6}{8} < \frac{7}{8}$.
This means $\frac{3}{4} < \frac{7}{8}$, which translates back to the original fractions:
$\frac{15}{20} < \frac{35}{40}$
The greater number is $\frac{35}{40}$.
Between the numbers $\frac{15}{20}$ and $\frac{35}{40}$ , the greater number is $\frac{35}{40}$.
Question 29. The reciprocal of a positive rational number is ___________.
Answer:
Let $x$ be a positive rational number.
By definition, a positive rational number can be written as $\frac{p}{q}$, where $p$ and $q$ are integers with the same sign (both positive or both negative), and $q \neq 0$. For example, $\frac{3}{4}$ or $\frac{-2}{-5}$.
The reciprocal of $x = \frac{p}{q}$ is $\frac{1}{x} = \frac{q}{p}$.
If $p$ and $q$ have the same sign, then the fraction $\frac{q}{p}$ also has a positive value.
For instance, if $x = \frac{3}{4}$, the reciprocal is $\frac{4}{3}$, which is positive.
If $x = \frac{-2}{-5}$, which is a positive rational number equivalent to $\frac{2}{5}$, its reciprocal is $\frac{-5}{-2}$, which is equivalent to $\frac{5}{2}$, also positive.
Also, the reciprocal of a rational number is also a rational number (provided the original number is non-zero, which a positive number is).
The reciprocal of a positive rational number is a positive rational number.
Question 30. The reciprocal of a negative rational number is ___________.
Answer:
Let $x$ be a negative rational number.
By definition, a negative rational number can be written as $\frac{p}{q}$, where $p$ and $q$ are integers with opposite signs, and $q \neq 0$. For example, $\frac{-3}{4}$ or $\frac{2}{-5}$.
The reciprocal of $x = \frac{p}{q}$ is $\frac{1}{x} = \frac{q}{p}$.
If $p$ and $q$ have opposite signs, then the fraction $\frac{q}{p}$ also has a negative value.
For instance, if $x = \frac{-3}{4}$, the reciprocal is $\frac{4}{-3}$, which is equivalent to $\frac{-4}{3}$, a negative rational number.
If $x = \frac{2}{-5}$, the reciprocal is $\frac{-5}{2}$, a negative rational number.
Also, the reciprocal of a rational number is also a rational number (provided the original number is non-zero, which a negative number is).
The reciprocal of a negative rational number is a negative rational number.
Question 31. Zero has ___________ reciprocal.
Answer:
The reciprocal of a number is its multiplicative inverse. For a non-zero number $a$, its reciprocal is $\frac{1}{a}$ such that $a \times \frac{1}{a} = 1$.
If we tried to find the reciprocal of 0, we would be looking for a number $y$ such that $0 \times y = 1$.
However, any number multiplied by 0 is 0 ($0 \times y = 0$).
Since $0 \neq 1$, there is no number $y$ that can satisfy the equation $0 \times y = 1$.
Therefore, the reciprocal of 0 does not exist.
Zero has no reciprocal.
Question 32. The numbers ___________ and ___________ are their own reciprocal.
Answer:
Let the number be $x$. Its reciprocal is $\frac{1}{x}$.
We are looking for numbers $x$ that are equal to their own reciprocal.
$x = \frac{1}{x}$
This equation is defined for $x \neq 0$.
Multiply both sides by $x$:
$x \times x = \frac{1}{x} \times x$
$x^2 = 1$
Taking the square root of both sides gives:
$\sqrt{x^2} = \sqrt{1}$
$|x| = 1$
This means $x$ can be $1$ or $-1$.
Check for $x=1$: The reciprocal of $1$ is $\frac{1}{1} = 1$. So, $1$ is its own reciprocal.
Check for $x=-1$: The reciprocal of $-1$ is $\frac{1}{-1} = -1$. So, $-1$ is its own reciprocal.
The numbers $1$ and $-1$ are their own reciprocal.
Question 33. If y be the reciprocal of x, then the reciprocal of y2 in terms of x will be ___________.
Answer:
We are given that $y$ is the reciprocal of $x$.
This means that $y = \frac{1}{x}$.
Also, this implies that $x \neq 0$ and $y \neq 0$.
We need to find the reciprocal of $y^2$ in terms of $x$.
First, let's express $y^2$ in terms of $x$:
$y^2 = \left(\frac{1}{x}\right)^2 = \frac{1^2}{x^2} = \frac{1}{x^2}$
Now, the reciprocal of $y^2$ is $\frac{1}{y^2}$.
Substitute the expression for $y^2$:
Reciprocal of $y^2 = \frac{1}{\left(\frac{1}{x^2}\right)}$
To divide by a fraction, we multiply by its reciprocal:
$\frac{1}{\left(\frac{1}{x^2}\right)} = 1 \times \frac{x^2}{1} = x^2$
So, the reciprocal of $y^2$ in terms of $x$ is $x^2$.
If y be the reciprocal of x, then the reciprocal of y2 in terms of x will be $x^2$.
Question 34. The reciprocal of $\frac{2}{5}$ × $\left( \frac{-4}{9} \right)$ is ___________.
Answer:
First, calculate the product of the given rational numbers:
$\frac{2}{5} \times \left( \frac{-4}{9} \right) = \frac{2 \times (-4)}{5 \times 9} = \frac{-8}{45}$
Now, find the reciprocal of the product $\frac{-8}{45}$.
The reciprocal of a non-zero rational number $\frac{a}{b}$ is $\frac{b}{a}$.
The reciprocal of $\frac{-8}{45}$ is $\frac{45}{-8}$.
This can also be written as $\frac{-45}{8}$.
The reciprocal of $\frac{2}{5} \times \left( \frac{-4}{9} \right)$ is $\frac{45}{-8}$ (or $\frac{-45}{8}$).
Question 35. (213 × 657)–1 = 213–1 × ___________.
Answer:
The property being illustrated here is related to the reciprocal of a product.
For any non-zero numbers $a$ and $b$, the reciprocal of their product $(a \times b)$ is equal to the product of their reciprocals $\frac{1}{a} \times \frac{1}{b}$.
In terms of exponents, the reciprocal of a number $x$ is $x^{-1}$.
So, the reciprocal of a product $(a \times b)$ is $(a \times b)^{-1}$.
The property states that $(a \times b)^{-1} = a^{-1} \times b^{-1}$.
In the given expression, we have $(213 \times 657)^{-1}$.
Using the property, this is equal to $213^{-1} \times 657^{-1}$.
The expression given is $(213 \times 657)^{–1} = 213^{–1} \times \text{___________}$.
Comparing this with the property $(a \times b)^{-1} = a^{-1} \times b^{-1}$, we can see that $a=213$ and $b=657$.
So, the missing term is $b^{-1} = 657^{-1}$.
(213 × 657)–1 = 213–1 × $657^{–1}$.
Question 36. The negative of 1 is ___________.
Answer:
The negative of a number is its additive inverse. The additive inverse of a number $a$ is the number $-a$ such that $a + (-a) = 0$.
We are asked for the negative of 1.
The negative of 1 is $-1$.
We can check this: $1 + (-1) = 0$.
The negative of 1 is $-1$.
Question 37. For rational numbers , $\frac{a}{b}$ , $\frac{c}{d}$ and $\frac{e}{f}$ we have $\frac{a}{b}\times\left( \frac{c}{d}+\frac{e}{f} \right)$ ) = _________ + ________.
Answer:
This question illustrates the distributive property of multiplication over addition for rational numbers.
The distributive property states that for any three numbers $x$, $y$, and $z$, the product of $x$ and the sum of $y$ and $z$ is equal to the sum of the products of $x$ and $y$, and $x$ and $z$.
Mathematically: $x \times (y + z) = (x \times y) + (x \times z)$.
In the given expression, we have $x = \frac{a}{b}$, $y = \frac{c}{d}$, and $z = \frac{e}{f}$.
Applying the distributive property:
$\frac{a}{b} \times \left( \frac{c}{d} + \frac{e}{f} \right) = \left( \frac{a}{b} \times \frac{c}{d} \right) + \left( \frac{a}{b} \times \frac{e}{f} \right)$
For rational numbers , $\frac{a}{b}$ , $\frac{c}{d}$ and $\frac{e}{f}$ we have $\frac{a}{b}\times\left( \frac{c}{d}+\frac{e}{f} \right)$ ) = $\frac{a}{b}\times\frac{c}{d}$ + $\frac{a}{b}\times\frac{e}{f}$.
Question 38. $\frac{-5}{7}$ is ________ than –3.
Answer:
To compare $\frac{-5}{7}$ and $-3$, we can express $-3$ as a fraction with a denominator of 7.
$-3 = \frac{-3 \times 7}{1 \times 7} = \frac{-21}{7}$
Now we compare $\frac{-5}{7}$ and $\frac{-21}{7}$.
When comparing two negative fractions with the same denominator, the fraction with the greater numerator is the greater number.
We compare $-5$ and $-21$.
$-5 > -21$ (since $-5$ is to the right of $-21$ on the number line).
Therefore, $\frac{-5}{7} > \frac{-21}{7}$.
This means $\frac{-5}{7}$ is greater than $-3$.
$\frac{-5}{7}$ is greater than –3.
Question 39. There are ________ rational numbers between any two rational numbers.
Answer:
The set of rational numbers is dense, which means that between any two distinct rational numbers, there is always another rational number. As demonstrated in Question 23, this process can be repeated infinitely many times.
There are infinitely many rational numbers between any two rational numbers.
Question 40. The rational numbers $\frac{1}{3}$ and $\frac{-1}{3}$ are on the ________ sides of zero on the number line.
Answer:
On the number line, positive numbers are located to the right of zero, and negative numbers are located to the left of zero.
The rational number $\frac{1}{3}$ is a positive number. Therefore, it is located to the right of zero.
The rational number $\frac{-1}{3}$ is a negative number. Therefore, it is located to the left of zero.
Since one number is to the right of zero and the other is to the left of zero, they are on opposite sides of zero.
The rational numbers $\frac{1}{3}$ and $\frac{-1}{3}$ are on the opposite sides of zero on the number line.
Question 41. The negative of a negative rational number is always a ________ rational number.
Answer:
Let the negative rational number be $r$. By definition, $r$ is a rational number and $r < 0$.
The "negative of $r$" is the additive inverse of $r$, which is $-r$.
We want to determine the sign of $-r$ when $r$ is a negative rational number.
If $r < 0$, multiplying both sides of the inequality by $-1$ reverses the inequality sign:
$(-1) \times r > (-1) \times 0$
$-r > 0$
Since $-r > 0$, the number $-r$ is a positive number.
For example, if the negative rational number is $-\frac{5}{7}$, its negative is $-\left(-\frac{5}{7}\right) = \frac{5}{7}$, which is a positive rational number.
If the negative rational number is $-2$, its negative is $-(-2) = 2$, which is a positive integer, and all integers are also rational numbers.
The negative of a negative rational number is always a positive rational number.
Question 42. Rational numbers can be added or multiplied in any __________.
Answer:
The property that allows numbers to be added or multiplied regardless of the order is called the commutative property.
For addition: $a + b = b + a$
For multiplication: $a \times b = b \times a$
This means we can change the order of the numbers in an addition or multiplication without changing the result.
Rational numbers possess this property for both addition and multiplication.
Rational numbers can be added or multiplied in any order.
Question 43. The reciprocal of $\frac{-5}{7}$ is ________.
Answer:
The reciprocal of a non-zero rational number $\frac{p}{q}$ is $\frac{q}{p}$.
The given rational number is $\frac{-5}{7}$.
To find its reciprocal, we swap the numerator and the denominator.
The reciprocal of $\frac{-5}{7}$ is $\frac{7}{-5}$.
We can also write this as $\frac{-7}{5}$.
To verify, multiply the number by its reciprocal:
$\frac{-5}{7} \times \frac{7}{-5} = \frac{(-5) \times 7}{7 \times (-5)} = \frac{-35}{-35} = 1$
The reciprocal of $\frac{-5}{7}$ is $\frac{7}{-5}$ (or $\frac{-7}{5}$).
Question 44. The multiplicative inverse of $\frac{4}{3}$ is _________.
Answer:
The multiplicative inverse of a non-zero rational number is the number which, when multiplied by the original number, gives a product of $1$.
For a rational number $\frac{a}{b}$ (where $a \neq 0$ and $b \neq 0$), its multiplicative inverse is $\frac{b}{a}$.
The given rational number is $\frac{4}{3}$.
Its multiplicative inverse is the reciprocal of $\frac{4}{3}$, which is obtained by swapping the numerator and the denominator.
Multiplicative inverse of $\frac{4}{3}$ is $\frac{3}{4}$.
We can verify this by multiplication:
$\frac{4}{3} \times \frac{3}{4} = \frac{4 \times 3}{3 \times 4} = \frac{12}{12} = 1$
The multiplicative inverse of $\frac{4}{3}$ is $\frac{3}{4}$.
Question 45. The rational number 10.11 in the from $\frac{p}{q}$ is _________.
Answer:
To express a terminating decimal as a rational number in the form $\frac{p}{q}$, we write the decimal number as a fraction with the decimal part over a power of 10.
The number 10.11 has two digits after the decimal point.
We can write it as:
$10.11 = 10 + 0.11$
$0.11 = \frac{11}{100}$ (since there are two decimal places, the denominator is $10^2 = 100$)
So, $10.11 = 10 + \frac{11}{100}$
To add a whole number and a fraction, we express the whole number as a fraction with the same denominator:
$10 = \frac{10 \times 100}{100} = \frac{1000}{100}$
Now, add the fractions:
$10.11 = \frac{1000}{100} + \frac{11}{100} = \frac{1000 + 11}{100} = \frac{1011}{100}$
The fraction $\frac{1011}{100}$ is in the form $\frac{p}{q}$, where $p=1011$ and $q=100$. Both are integers and $q \neq 0$.
We should check if the fraction can be simplified by finding the greatest common divisor (GCD) of 1011 and 100.
Prime factorization of 100 is $2^2 \times 5^2$. The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, 100.
Check if 1011 is divisible by 2, 4, 5, 10, etc.
1011 is not divisible by 2 (it's odd).
The sum of the digits of 1011 is $1+0+1+1 = 3$, which is divisible by 3. So, 1011 is divisible by 3.
$1011 \div 3 = 337$.
So, $1011 = 3 \times 337$.
337 is not divisible by 2, 3, 5. Let's check for other prime factors of 100. None exist apart from 2 and 5. Thus, there is no common factor between 1011 and 100 other than 1.
The fraction $\frac{1011}{100}$ is already in its simplest form.
The rational number 10.11 in the from $\frac{p}{q}$ is $\frac{1011}{100}$.
Question 46. $\frac{1}{5}$ × $\left[ \frac{2}{7} + \frac{3}{8} \right]$ = $\left[ \frac{1}{5} × \frac{2}{7} \right]$ + ___________.
Answer:
This equation is an example of the distributive property of multiplication over addition for rational numbers.
The distributive property states that for any three rational numbers $a$, $b$, and $c$:
$a \times (b + c) = (a \times b) + (a \times c)$
In the given equation, we have:
$a = \frac{1}{5}$
$b = \frac{2}{7}$
$c = \frac{3}{8}$
Applying the distributive property to the left side of the equation:
$\frac{1}{5} \times \left[ \frac{2}{7} + \frac{3}{8} \right] = \left( \frac{1}{5} \times \frac{2}{7} \right) + \left( \frac{1}{5} \times \frac{3}{8} \right)$
Comparing this with the given equation $\frac{1}{5}$ × $\left[ \frac{2}{7} + \frac{3}{8} \right]$ = $\left[ \frac{1}{5} × \frac{2}{7} \right]$ + ___________, the blank must be the second term on the right side.
The second term is $\left( \frac{1}{5} \times \frac{3}{8} \right)$.
So, the completed equation is:
$\frac{1}{5}$ × $\left[ \frac{2}{7} + \frac{3}{8} \right]$ = $\left[ \frac{1}{5} × \frac{2}{7} \right]$ + $\left[ \frac{1}{5} × \frac{3}{8} \right]$.
Question 47. The two rational numbers lying between –2 and –5 with denominator as 1 are _________ and _________.
Answer:
The rational numbers are given as $-2$ and $-5$.
We can write these numbers with a denominator of 1:
$-2 = \frac{-2}{1}$
$-5 = \frac{-5}{1}$
We are looking for rational numbers between $-2$ and $-5$ with a denominator of 1.
The numbers between $-2$ and $-5$ on the number line are $-3$ and $-4$.
We can express these integers as rational numbers with a denominator of 1:
$-3 = \frac{-3}{1}$
$-4 = \frac{-4}{1}$
Checking the order on the number line: $-5 < -4 < -3 < -2$.
So, the rational numbers between $-2$ and $-5$ with a denominator of 1 are $\frac{-3}{1}$ and $\frac{-4}{1}$.
The two rational numbers lying between –2 and –5 with denominator as 1 are $\frac{-3}{1}$ and $\frac{-4}{1}$ (or simply -3 and -4).
Question 48 to 99 (True or False)
In each of the following, state whether the statements are true (T) or false (F).
Question 48. If $\frac{x}{y}$ is a rational number, then y is always a whole number.
Answer:
False (F)
A rational number is defined as a number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
In the given statement, $\frac{x}{y}$ is a rational number. According to the definition, this means $x$ and $y$ must be integers, and $y$ must not be equal to $0$.
The set of whole numbers is $\{0, 1, 2, 3, \dots\}$. The set of integers includes positive integers, negative integers, and zero ($\dots, -2, -1, 0, 1, 2, \dots$).
While all positive integers are whole numbers, negative integers are not whole numbers. The definition of a rational number requires the denominator $y$ to be a non-zero integer, which can be positive or negative.
For example, consider the rational number $\frac{1}{-3}$. Here, $x = 1$ and $y = -3$. Both $1$ and $-3$ are integers, and $-3 \neq 0$. So, $\frac{1}{-3}$ is a rational number.
However, the denominator $y = -3$ is a negative integer, which is not a whole number.
Therefore, if $\frac{x}{y}$ is a rational number, $y$ is always a non-zero integer, but not necessarily a whole number.
Question 49. If $\frac{p}{q}$ is a rational number, then p cannot be equal to zero.
Answer:
False (F)
A rational number is defined as a number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
The definition of a rational number puts a restriction on the denominator $q$ (it cannot be zero), but it does not put any restriction on the numerator $p$. The numerator $p$ can be any integer, including zero.
For example, $\frac{0}{5}$ is a rational number because $0$ is an integer, $5$ is an integer, and $5 \neq 0$. The value of $\frac{0}{5}$ is $0$, which is a rational number.
Therefore, the numerator $p$ of a rational number $\frac{p}{q}$ can be equal to zero.
Question 50. If $\frac{r}{s}$ is a rational number, then s cannot be equal to zero.
Answer:
True (T)
A rational number is defined as a number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
In the given statement, $\frac{r}{s}$ is a rational number. For $\frac{r}{s}$ to be a rational number, $r$ and $s$ must be integers, and the denominator $s$ must satisfy the condition $s \neq 0$.
The statement "then s cannot be equal to zero" is precisely the condition required for the denominator of a rational number.
Therefore, if $\frac{r}{s}$ is a rational number, it is necessary that $s$ is not equal to zero.
Question 51. $\frac{5}{6}$ lies between $\frac{2}{3}$ and 1.
Answer:
True (T)
To check if $\frac{5}{6}$ lies between $\frac{2}{3}$ and 1, we need to compare the values of these three numbers.
The numbers are $\frac{2}{3}$, $\frac{5}{6}$, and $1$.
To compare fractions, we can find a common denominator. The least common multiple of the denominators 3, 6, and 1 is 6.
Convert each number to an equivalent fraction with a denominator of 6:
$\frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}$
$\frac{5}{6} = \frac{5}{6}$
$1 = \frac{1}{1} = \frac{1 \times 6}{1 \times 6} = \frac{6}{6}$
Now compare the numerators of the fractions with the same denominator:
4, 5, 6
Since $4 < 5 < 6$, we have:
$\frac{4}{6} < \frac{5}{6} < \frac{6}{6}$
Substituting the original numbers back:
$\frac{2}{3} < \frac{5}{6} < 1$
This shows that $\frac{5}{6}$ is greater than $\frac{2}{3}$ and less than 1.
Therefore, $\frac{5}{6}$ lies between $\frac{2}{3}$ and 1.
Question 52. $\frac{5}{10}$ lies between $\frac{1}{2}$ and 1.
Answer:
False (F)
To check if $\frac{5}{10}$ lies between $\frac{1}{2}$ and 1, we first simplify the fraction $\frac{5}{10}$.
$\frac{5}{10} = \frac{5 \div 5}{10 \div 5} = \frac{1}{2}$
So the statement is equivalent to asking if $\frac{1}{2}$ lies between $\frac{1}{2}$ and 1.
For a number to lie strictly between two other numbers, it must be greater than the smaller number and less than the larger number.
In this case, the range is from $\frac{1}{2}$ to 1.
The number is $\frac{1}{2}$.
We need to check if $\frac{1}{2} < \frac{1}{2}$ and $\frac{1}{2} < 1$.
The first inequality, $\frac{1}{2} < \frac{1}{2}$, is false because $\frac{1}{2}$ is equal to $\frac{1}{2}$, not strictly less than it.
The second inequality, $\frac{1}{2} < 1$, is true.
Since $\frac{1}{2}$ is not strictly greater than the lower bound ($\frac{1}{2}$), it does not lie *between* $\frac{1}{2}$ and 1.
It is one of the boundary points, but not strictly between them.
Question 53. $\frac{-7}{2}$ lies between –3 and –4.
Answer:
True (T)
To determine if $\frac{-7}{2}$ lies between –3 and –4, we can convert $\frac{-7}{2}$ to a decimal or a mixed number.
$\frac{-7}{2} = -3.5$
Now we need to check if $-3.5$ lies between –3 and –4.
On the number line, numbers increase from left to right. The order of –3 and –4 is that –4 is to the left of –3, meaning $-4 < -3$.
For $-3.5$ to lie between –4 and –3, it must be greater than –4 and less than –3.
We check the inequalities:
$-4 < -3.5$
$-3.5 < -3$
Both inequalities are true.
Therefore, $-3.5$, which is $\frac{-7}{2}$, lies between –4 and –3.
Question 54. $\frac{9}{6}$ lies between 1 and 2.
Answer:
True (T)
To check if $\frac{9}{6}$ lies between 1 and 2, we can first simplify the fraction $\frac{9}{6}$.
$\frac{9}{6} = \frac{9 \div 3}{6 \div 3} = \frac{3}{2}$
Now the question is whether $\frac{3}{2}$ lies between 1 and 2.
We can convert $\frac{3}{2}$ to a decimal or a mixed number:
$\frac{3}{2} = 1.5$ or $1\frac{1}{2}$.
For a number to lie between 1 and 2, it must be greater than 1 and less than 2.
We check the inequalities:
$1 < 1.5$
$1.5 < 2$
Both inequalities are true.
Since $1 < 1.5 < 2$, the number $1.5$, which is $\frac{9}{6}$, lies between 1 and 2.
Question 55. If a ≠ 0, the multiplicative inverse of $\frac{a}{b}$ is $\frac{b}{a}$ .
Answer:
True (T)
The multiplicative inverse of a non-zero number is the number which, when multiplied by the original number, gives a product of 1.
For a rational number $\frac{a}{b}$, its multiplicative inverse is $\frac{b}{a}$, provided that $\frac{a}{b}$ is not equal to zero (i.e., $a \neq 0$) and the denominator $b$ is also not equal to zero (for the original fraction to be defined).
The statement says $a \neq 0$. Assuming $b \neq 0$ (which is required for $\frac{a}{b}$ to be a valid rational number), we can find the multiplicative inverse.
Let the multiplicative inverse of $\frac{a}{b}$ be $X$. Then, according to the definition:
$\frac{a}{b} \times X = 1$
To find $X$, we can multiply both sides by $\frac{b}{a}$ (which is valid since $a \neq 0$).
$\left(\frac{b}{a}\right) \times \left(\frac{a}{b} \times X\right) = \left(\frac{b}{a}\right) \times 1$
$\left(\frac{b}{a} \times \frac{a}{b}\right) \times X = \frac{b}{a}$
$\frac{ba}{ab} \times X = \frac{b}{a}$
$1 \times X = \frac{b}{a}$
$X = \frac{b}{a}$
Also, we can directly check the product of $\frac{a}{b}$ and $\frac{b}{a}$:
$\frac{a}{b} \times \frac{b}{a} = \frac{a \times b}{b \times a} = \frac{ab}{ab}$
Since $a \neq 0$ and we assume $b \neq 0$, $ab \neq 0$. Therefore, $\frac{ab}{ab} = 1$.
This confirms that $\frac{b}{a}$ is the multiplicative inverse of $\frac{a}{b}$ when $a \neq 0$ (and $b \neq 0$).
Question 56. The multiplicative inverse of $\frac{-3}{5}$ is $\frac{5}{3}$
Answer:
False (F)
The multiplicative inverse of a non-zero number is the number which, when multiplied by the original number, results in a product of 1.
Let the given number be $\frac{-3}{5}$.
The statement claims that the multiplicative inverse is $\frac{5}{3}$.
Let's multiply the number $\frac{-3}{5}$ by the claimed inverse $\frac{5}{3}$:
Product $= \frac{-3}{5} \times \frac{5}{3}$
Product $= \frac{(-3) \times 5}{5 \times 3}$
Product $= \frac{-15}{15}$
Product $= -1$
Since the product is $-1$ and not $1$, $\frac{5}{3}$ is not the multiplicative inverse of $\frac{-3}{5}$.
The correct multiplicative inverse of $\frac{-3}{5}$ is its reciprocal, which is $\frac{5}{-3}$ or $\frac{-5}{3}$.
Check the correct inverse: $\frac{-3}{5} \times \frac{-5}{3} = \frac{(-3) \times (-5)}{5 \times 3} = \frac{15}{15} = 1$.
Therefore, the statement is false.
Question 57. The additive inverse of $\frac{1}{2}$ is –2.
Answer:
False (F)
The additive inverse of a number is the number which, when added to the original number, results in a sum of 0.
Let the given number be $\frac{1}{2}$.
Let the additive inverse of $\frac{1}{2}$ be $y$. According to the definition:
$\frac{1}{2} + y = 0$
To find $y$, we subtract $\frac{1}{2}$ from both sides:
$y = 0 - \frac{1}{2}$
$y = -\frac{1}{2}$
The additive inverse of $\frac{1}{2}$ is $-\frac{1}{2}$.
The statement claims that the additive inverse is –2.
Comparing $-\frac{1}{2}$ and –2, we see that they are not the same number.
$-\frac{1}{2} = -0.5$
$-2 = -2.0$
Since $-0.5 \neq -2.0$, the statement is false.
Question 58. If $\frac{x}{y}$ is the additive inverse of $\frac{c}{d}$ , then $\frac{x}{y}$ + $\frac{c}{d}$ = 0.
Answer:
True (T)
The additive inverse of a number is defined as the number which, when added to the original number, gives a sum of 0.
If $\frac{x}{y}$ is the additive inverse of $\frac{c}{d}$, it means that adding $\frac{x}{y}$ to $\frac{c}{d}$ results in 0.
By the definition of additive inverse, this precisely means:
$\frac{c}{d} + \frac{x}{y} = 0$
Or, as stated in the question (due to the commutative property of addition):
$\frac{x}{y} + \frac{c}{d} = 0$
Therefore, the statement directly reflects the definition of additive inverses and is true.
Question 59. For every rational number x, x + 1 = x.
Answer:
False (F)
The given statement is that for every rational number $x$, the equation $x + 1 = x$ is true.
Let's analyze the equation:
$x + 1 = x$
To solve for $x$, we can subtract $x$ from both sides of the equation:
$(x + 1) - x = x - x$
Simplifying both sides gives:
$1 = 0$
The resulting equation $1 = 0$ is a false statement.
Since the equation $x + 1 = x$ simplifies to a false statement that does not depend on $x$, it means there is no value of $x$ for which the original equation is true.
Therefore, the statement "$x + 1 = x$ for every rational number $x$" is false.
Question 60. If $\frac{x}{y}$ is the additive inverse of $\frac{c}{d}$ , then $\frac{x}{y}$ - $\frac{c}{d}$ = 0.
Answer:
False (F)
The additive inverse of a number is the number which, when added to the original number, results in a sum of 0.
If $\frac{x}{y}$ is the additive inverse of $\frac{c}{d}$, this means that their sum is 0.
So, according to the definition:
$\frac{x}{y} + \frac{c}{d} = 0$
This equation implies that $\frac{x}{y} = -\frac{c}{d}$.
Now let's look at the statement given in the question: $\frac{x}{y} - \frac{c}{d} = 0$.
Substitute the relationship $\frac{x}{y} = -\frac{c}{d}$ into this statement:
$(-\frac{c}{d}) - \frac{c}{d} = 0$
$-\frac{c}{d} - \frac{c}{d} = 0$
$-2 \times \frac{c}{d} = 0$
This resulting equation, $-2 \times \frac{c}{d} = 0$, is only true if $\frac{c}{d} = 0$.
However, $\frac{c}{d}$ can be any rational number. For the concept of additive inverse to be applicable to $\frac{c}{d}$, it just needs to be a rational number (which can be 0). The definition of additive inverse $\frac{x}{y}$ of $\frac{c}{d}$ means $\frac{x}{y} = -\frac{c}{d}$.
Let's take an example where $\frac{c}{d} \neq 0$.
Suppose $\frac{c}{d} = \frac{1}{2}$. Its additive inverse $\frac{x}{y}$ is $-\frac{1}{2}$.
According to the statement, we should have $\frac{x}{y} - \frac{c}{d} = 0$.
Substituting the values:
$(-\frac{1}{2}) - (\frac{1}{2}) = -\frac{1}{2} - \frac{1}{2} = -\left(\frac{1}{2} + \frac{1}{2}\right) = -1$
Since $-1 \neq 0$, the statement $\frac{x}{y} - \frac{c}{d} = 0$ is not true for all cases where $\frac{x}{y}$ is the additive inverse of $\frac{c}{d}$.
The correct relationship for additive inverses is that their sum is 0, not their difference.
Question 61. The reciprocal of a non-zero rational number $\frac{q}{p}$ is the rational number $\frac{q}{p}$ .
Answer:
False (F)
The reciprocal (or multiplicative inverse) of a non-zero number is the number which, when multiplied by the original number, gives a product of 1.
Let the given non-zero rational number be $\frac{q}{p}$. Since it's a non-zero rational number, it means $q$ and $p$ are integers, $p \neq 0$, and importantly, $q \neq 0$ (otherwise the number itself would be zero).
The statement claims that the reciprocal of $\frac{q}{p}$ is $\frac{q}{p}$.
Let's multiply the number by the claimed reciprocal:
$\frac{q}{p} \times \frac{q}{p} = \frac{q \times q}{p \times p} = \frac{q^2}{p^2}$
For $\frac{q}{p}$ to be its own reciprocal, this product must be equal to 1:
$\frac{q^2}{p^2} = 1$
$q^2 = p^2$
This equation is true only if $q = p$ or $q = -p$.
For example, if $\frac{q}{p} = \frac{2}{3}$, then $q=2$ and $p=3$. $q^2 = 4$ and $p^2 = 9$. $\frac{q^2}{p^2} = \frac{4}{9} \neq 1$. The reciprocal of $\frac{2}{3}$ is $\frac{3}{2}$.
The only non-zero rational numbers that are equal to their own reciprocals are 1 and -1. For these numbers, $q=p$ (for 1) or $q=-p$ (for -1), which satisfies $q^2 = p^2$.
The statement says the reciprocal of *a* non-zero rational number $\frac{q}{p}$ is $\frac{q}{p}$. This implies it is true for *every* non-zero rational number, which is not the case.
The correct reciprocal of a non-zero rational number $\frac{q}{p}$ is $\frac{p}{q}$ (provided $p \neq 0$ and $q \neq 0$).
Question 62. If x + y = 0, then –y is known as the negative of x, where x and y are rational numbers.
Answer:
False (F)
The negative (or additive inverse) of a rational number $x$ is defined as the number $-x$, such that $x + (-x) = 0$.
We are given the condition $x + y = 0$. From this equation, we can determine that $y = -x$. This means $y$ is the negative of $x$.
The statement claims that "$-y$ is known as the negative of $x$". This means it claims that $-y = -x$.
Let's check if the given condition $x+y=0$ implies $-y = -x$.
We know $y = -x$ from the condition $x+y=0$.
Substitute $y = -x$ into the claim $-y = -x$:
$-(-x) = -x$
$x = -x$
This equation $x = -x$ is equivalent to $2x = 0$, which is only true when $x = 0$.
The condition $x+y=0$ holds true for any pair of rational numbers where one is the negative of the other (e.g., $x=2, y=-2$). The statement is not true for all such pairs (e.g., if $x=2$, then $-y = -(-2) = 2$, and the negative of $x$ is $-2$; $2 \neq -2$).
Therefore, the statement is false because $-y$ is equal to $x$, and $x$ is only the negative of $x$ when $x=0$.
Question 63. The negative of the negative of any rational number is the number itself.
Answer:
True (T)
Let $x$ be any rational number.
The negative of a number $x$ is denoted by $-x$. It is the number such that $x + (-x) = 0$.
The statement asks about the negative of the negative of $x$. This can be written as $-(-x)$.
We know that the sum of a number and its negative is 0. So, for the number $-x$, its negative is the number that, when added to $-x$, gives 0.
We are looking for the value of $-(-x)$. By definition, this is the additive inverse of $-x$.
We know that $x + (-x) = 0$.
This equation shows that $x$ is the additive inverse of $-x$.
Therefore, $-(-x) = x$.
This property holds true for all rational numbers. The negative of the negative of any rational number is indeed the number itself.
Question 64. The negative of 0 does not exist.
Answer:
False (F)
The negative of a number (also called the additive inverse) is the number which, when added to the original number, results in a sum of 0.
Let's find the negative of 0. Let the negative of 0 be represented by the variable $n$. According to the definition, we have:
$0 + n = 0$
Solving this equation for $n$, we find:
$n = 0 - 0$
$n = 0$
This shows that the negative of 0 is 0 itself.
Since we found a number (which is 0) that fits the definition of the negative of 0, the negative of 0 does exist.
Therefore, the statement "The negative of 0 does not exist" is false.
Question 65. The negative of 1 is 1 itself.
Answer:
False (F)
The negative of a number (also known as the additive inverse) is the number which, when added to the original number, results in a sum of 0.
We want to find the negative of 1. Let the negative of 1 be represented by $n$. According to the definition, we have:
$1 + n = 0$
To find $n$, we subtract 1 from both sides of the equation:
$n = 0 - 1$
$n = -1$
So, the negative of 1 is $-1$.
The statement claims that the negative of 1 is 1 itself.
Comparing the result, $-1$, with the claimed value, $1$, we see that $-1 \neq 1$.
Therefore, the statement "The negative of 1 is 1 itself" is false.
Question 66. For all rational numbers x and y, x – y = y – x.
Answer:
False (F)
The statement claims that for all rational numbers $x$ and $y$, subtraction is commutative, i.e., $x - y = y - x$.
Let's test this property with an example using rational numbers.
Let $x = 5$ and $y = 3$. Both 5 and 3 are rational numbers.
Calculate $x - y$:
$x - y = 5 - 3 = 2$
Calculate $y - x$:
$y - x = 3 - 5 = -2$
Comparing the results, we see that $2 \neq -2$.
Thus, $x - y \neq y - x$ for $x=5$ and $y=3$.
The equation $x - y = y - x$ is only true when $x = y$. For example, if $x=5$ and $y=5$, then $x-y = 5-5=0$ and $y-x = 5-5=0$. However, the statement claims it is true for *all* rational numbers $x$ and $y$.
Since we found a case where the statement is false, the statement "For all rational numbers x and y, x – y = y – x" is false.
Subtraction is not a commutative operation for rational numbers (or indeed for most number systems).
Question 67. For all rational numbers x and y, x × y = y × x.
Answer:
True (T)
The statement claims that for all rational numbers $x$ and $y$, the equation $x \times y = y \times x$ is true. This property is known as the commutative property of multiplication.
Rational numbers are numbers that can be expressed as a fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
Let $x = \frac{a}{b}$ and $y = \frac{c}{d}$, where $a, b, c, d$ are integers and $b \neq 0$, $d \neq 0$.
Calculate $x \times y$:
$x \times y = \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}$
Calculate $y \times x$:
$y \times x = \frac{c}{d} \times \frac{a}{b} = \frac{c \times a}{d \times b}$
Since multiplication of integers is commutative (i.e., $a \times c = c \times a$ and $b \times d = d \times b$), we have:
$\frac{a \times c}{b \times d} = \frac{c \times a}{d \times b}$
Therefore, $\frac{a}{b} \times \frac{c}{d} = \frac{c}{d} \times \frac{a}{b}$.
This means that $x \times y = y \times x$ for all rational numbers $x$ and $y$.
Multiplication is indeed commutative for rational numbers.
Question 68. For every rational number x, x × 0 = x.
Answer:
False (F)
The given statement is that for every rational number $x$, the equation $x \times 0 = x$ is true.
According to the property of multiplication by zero, any number multiplied by 0 is equal to 0.
$x \times 0 = 0$
The statement $x \times 0 = x$ can therefore be rewritten as:
$0 = x$
This means the original equation $x \times 0 = x$ is only true if $x$ is equal to 0.
The statement claims that this is true for *every* rational number $x$.
Let's consider a rational number other than 0, for example, $x = \frac{1}{2}$.
According to the statement, $\frac{1}{2} \times 0$ should be equal to $\frac{1}{2}$.
$\frac{1}{2} \times 0 = 0$
We see that $0 \neq \frac{1}{2}$.
Since the equation $x \times 0 = x$ is not true for $x = \frac{1}{2}$ (and for any rational number other than 0), the statement "For every rational number x, x × 0 = x" is false.
Question 69. For every rational numbers x, y and z, x + (y × z) = (x + y) × (x + z).
Answer:
False (F)
The statement claims that for all rational numbers $x$, $y$, and $z$, the equation $x + (y \times z) = (x + y) \times (x + z)$ is true.
Let's test this statement with a specific example using rational numbers. Let $x = 1$, $y = 2$, and $z = 3$. These are all rational numbers.
Calculate the Left Hand Side (LHS) of the equation:
$LHS = x + (y \times z)$
$LHS = 1 + (2 \times 3)$
$LHS = 1 + 6$
$LHS = 7$
Now calculate the Right Hand Side (RHS) of the equation:
$RHS = (x + y) \times (x + z)$
$RHS = (1 + 2) \times (1 + 3)$
$RHS = 3 \times 4$
$RHS = 12$
Comparing the LHS and RHS, we find $7 \neq 12$.
Since the equation $x + (y \times z) = (x + y) \times (x + z)$ does not hold true for this specific set of rational numbers ($x=1, y=2, z=3$), it is not true for *every* rational number.
Therefore, the statement is false. This property is not a general property of rational numbers.
Question 70. For all rational numbers a, b and c, a(b + c) = ab + bc.
Answer:
False (F)
The statement claims that for all rational numbers $a$, $b$, and $c$, the equation $a(b + c) = ab + bc$ is true.
This equation represents the distributive property of multiplication over addition. However, the property states that $a(b + c) = ab + ac$.
Let's test the given statement with a specific example using rational numbers. Let $a = 2$, $b = 3$, and $c = 4$. These are all rational numbers.
Calculate the Left Hand Side (LHS) of the given equation:
$LHS = a(b + c)$
$LHS = 2(3 + 4)$
$LHS = 2(7)$
$LHS = 14$
Now calculate the Right Hand Side (RHS) of the given equation:
$RHS = ab + bc$
$RHS = (2 \times 3) + (3 \times 4)$
$RHS = 6 + 12$
$RHS = 18$
Comparing the LHS and RHS, we find $14 \neq 18$.
Since the equation $a(b + c) = ab + bc$ does not hold true for this specific set of rational numbers ($a=2, b=3, c=4$), it is not true for *every* rational number.
The correct distributive property is $a(b + c) = ab + ac$. If the statement was $a(b+c) = ab+ac$, it would be true.
Therefore, the statement as given is false.
Question 71. 1 is the only number which is its own reciprocal.
Answer:
False (F)
The reciprocal of a non-zero number $x$ is the number $y$ such that $x \times y = 1$.
For a number $x$ to be its own reciprocal, the number must be equal to its reciprocal. This means:
$x \times x = 1$
$x^2 = 1$
We need to find all rational numbers $x$ that satisfy this equation.
Subtracting 1 from both sides:
$x^2 - 1 = 0$
Factoring the difference of squares:
$(x - 1)(x + 1) = 0$
For this product to be zero, one or both of the factors must be zero.
Case 1: $x - 1 = 0$
$x = 1$
Case 2: $x + 1 = 0$
$x = -1$
Both $x = 1$ and $x = -1$ are rational numbers, and they both satisfy the condition $x^2 = 1$.
- For $x=1$, the reciprocal is $\frac{1}{1} = 1$. So 1 is its own reciprocal.
- For $x=-1$, the reciprocal is $\frac{1}{-1} = -1$. So -1 is its own reciprocal.
Since both 1 and -1 are their own reciprocals, the statement that 1 is the *only* such number is false.
Question 72. –1 is not the reciprocal of any rational number.
Answer:
False (F)
The reciprocal of a non-zero rational number $x$ is the number $\frac{1}{x}$. When a number is multiplied by its reciprocal, the product is 1.
The statement claims that –1 is not the reciprocal of any rational number. To check this, let's see if there exists a rational number $x$ such that its reciprocal is –1.
Let the reciprocal of a rational number $x$ be –1. By definition of a reciprocal, this means:
$x \times (-1) = 1$
To find $x$, we can divide both sides by –1:
$x = \frac{1}{-1}$
$x = -1$
We found that the number whose reciprocal is –1 is –1 itself.
Is –1 a rational number? Yes, –1 can be expressed as $\frac{-1}{1}$, where -1 and 1 are integers and the denominator is non-zero.
Since –1 is a rational number, and its reciprocal is –1, this means –1 is the reciprocal of a rational number (namely, –1).
Therefore, the statement "–1 is not the reciprocal of any rational number" is false.
Question 73. For any rational number x, x + (–1) = –x.
Answer:
False (F)
The statement claims that for every rational number $x$, the equation $x + (-1) = -x$ is true.
Adding $-1$ to a number is the same as subtracting 1 from it. So the equation can be rewritten as:
$x - 1 = -x$
To see if this equation is true for all rational numbers, let's try to solve for $x$.
Add $x$ to both sides of the equation:
$x - 1 + x = -x + x$
$2x - 1 = 0$
Now, add 1 to both sides:
$2x = 1$
Finally, divide by 2:
$x = \frac{1}{2}$
This means that the original equation $x + (-1) = -x$ is only true when $x$ is equal to $\frac{1}{2}$.
The statement asserts that this equality holds for any rational number $x$. However, we found that it is only true for a specific value of $x$, namely $\frac{1}{2}$.
For instance, if we take a rational number $x = 3$ (which is a rational number):
LHS = $x + (-1) = 3 + (-1) = 3 - 1 = 2$
RHS = $-x = -3$
Since $2 \neq -3$, the statement is false for $x = 3$.
Therefore, the statement "For any rational number x, x + (–1) = –x" is false.
Question 74. For rational numbers x and y, if x < y then x – y is a positive rational number.
Answer:
False (F)
The statement claims that if we have two rational numbers $x$ and $y$ such that $x < y$, then their difference $x - y$ is a positive rational number.
Let's analyze the inequality $x < y$.
If we subtract $y$ from both sides of the inequality, the direction of the inequality remains the same:
$x - y < y - y$
This simplifies to:
$x - y < 0$
The expression $x - y < 0$ means that the difference $x - y$ is a negative number.
For example, let $x = 2$ and $y = 5$. Both are rational numbers, and $2 < 5$.
According to the statement, $x - y$ should be positive.
$x - y = 2 - 5 = -3$
The result, $-3$, is a negative rational number, not a positive one.
Thus, if $x < y$, the difference $x - y$ is always a negative rational number.
Therefore, the statement "For rational numbers x and y, if x < y then x – y is a positive rational number" is false.
Question 75. If x and y are negative rational numbers, then so is x + y.
Answer:
True (T)
Let $x$ and $y$ be negative rational numbers.
This means that $x$ is a rational number and $x < 0$.
This also means that $y$ is a rational number and $y < 0$.
We need to determine if the sum $x + y$ is also a negative rational number.
We know that the sum of two rational numbers is always a rational number. So, $x+y$ is a rational number.
Now let's consider the sign of the sum. We have the inequalities:
$x < 0$
$y < 0$
Adding these two inequalities, we get:
$x + y < 0 + 0$
$x + y < 0$
Since $x + y < 0$, this means that the sum $x + y$ is a negative number.
Therefore, if $x$ and $y$ are negative rational numbers, their sum $x + y$ is a negative rational number.
For example, let $x = -\frac{1}{2}$ and $y = -\frac{1}{4}$. Both are negative rational numbers.
$x + y = -\frac{1}{2} + (-\frac{1}{4}) = -\frac{2}{4} - \frac{1}{4} = -\frac{3}{4}$
$-\frac{3}{4}$ is a rational number and $-\frac{3}{4} < 0$.
Question 76. Between any two rational numbers there are exactly ten rational numbers.
Answer:
False (F)
This statement is false because between any two distinct rational numbers, there are infinitely many rational numbers.
This is a property known as the density of rational numbers.
Given any two distinct rational numbers, say $r_1$ and $r_2$, where $r_1 < r_2$, we can always find another rational number between them. For example, their average $\frac{r_1 + r_2}{2}$ is always a rational number and lies between $r_1$ and $r_2$ ($r_1 < \frac{r_1 + r_2}{2} < r_2$).
We can repeat this process infinitely many times. We can find a rational number between $r_1$ and $\frac{r_1 + r_2}{2}$, another between $\frac{r_1 + r_2}{2}$ and $r_2$, and so on.
Since we can continue finding new rational numbers between any two existing ones indefinitely, there cannot be a fixed, finite number of rational numbers (like exactly ten) between any two given rational numbers.
Question 77. Rational numbers are closed under addition and multiplication but not under subtraction.
Answer:
False (F)
A set of numbers is said to be closed under an operation if performing that operation on any two numbers from the set always results in a number that is also in the set.
Let's examine closure for rational numbers under the three operations mentioned:
1. Closure under Addition:
If $x$ and $y$ are any two rational numbers, is $x+y$ always a rational number?
Let $x = \frac{a}{b}$ and $y = \frac{c}{d}$, where $a, b, c, d$ are integers and $b \neq 0, d \neq 0$.
$x + y = \frac{a}{b} + \frac{c}{d} = \frac{ad + bc}{bd}$.
Since $a, b, c, d$ are integers, $ad$, $bc$, and $ad+bc$ are integers. Since $b \neq 0$ and $d \neq 0$, $bd \neq 0$. The result $\frac{ad + bc}{bd}$ is in the form $\frac{\text{integer}}{\text{non-zero integer}}$, which is a rational number.
Thus, rational numbers are closed under addition. This part of the statement is correct.
2. Closure under Multiplication:
If $x$ and $y$ are any two rational numbers, is $x \times y$ always a rational number?
Let $x = \frac{a}{b}$ and $y = \frac{c}{d}$, where $a, b, c, d$ are integers and $b \neq 0, d \neq 0$.
$x \times y = \frac{a}{b} \times \frac{c}{d} = \frac{ac}{bd}$.
Since $a, c$ are integers, $ac$ is an integer. Since $b, d$ are integers, $bd$ is an integer. Since $b \neq 0$ and $d \neq 0$, $bd \neq 0$. The result $\frac{ac}{bd}$ is in the form $\frac{\text{integer}}{\text{non-zero integer}}$, which is a rational number.
Thus, rational numbers are closed under multiplication. This part of the statement is correct.
3. Closure under Subtraction:
If $x$ and $y$ are any two rational numbers, is $x - y$ always a rational number?
Let $x = \frac{a}{b}$ and $y = \frac{c}{d}$, where $a, b, c, d$ are integers and $b \neq 0, d \neq 0$.
$x - y = \frac{a}{b} - \frac{c}{d} = \frac{ad - bc}{bd}$.
Since $a, b, c, d$ are integers, $ad$, $bc$, and $ad-bc$ are integers. Since $b \neq 0$ and $d \neq 0$, $bd \neq 0$. The result $\frac{ad - bc}{bd}$ is in the form $\frac{\text{integer}}{\text{non-zero integer}}$, which is a rational number.
Thus, rational numbers are closed under subtraction.
The statement claims that rational numbers are *not* closed under subtraction. This is false.
Rational numbers are closed under addition, subtraction, and multiplication (and division by a non-zero rational number).
Question 78. Subtraction of rational number is commutative.
Answer:
False (F)
An operation is commutative if changing the order of the operands does not change the result. For subtraction of rational numbers, this would mean that for any two rational numbers $x$ and $y$, the following equality holds:
$x - y = y - x$
Let's test this with an example. Consider the rational numbers $x = \frac{1}{2}$ and $y = \frac{1}{3}$.
Calculate $x - y$:
$x - y = \frac{1}{2} - \frac{1}{3} = \frac{3}{6} - \frac{2}{6} = \frac{3 - 2}{6} = \frac{1}{6}$
Calculate $y - x$:
$y - x = \frac{1}{3} - \frac{1}{2} = \frac{2}{6} - \frac{3}{6} = \frac{2 - 3}{6} = \frac{-1}{6}$
Comparing the results, we see that $\frac{1}{6} \neq \frac{-1}{6}$.
Since we found a case where $x - y \neq y - x$, subtraction is not a commutative operation for rational numbers.
Question 79. $\frac{-3}{4}$ is smaller than –2.
Answer:
False (F)
To compare the rational number $\frac{-3}{4}$ with the integer –2 (which is also a rational number), we can convert $\frac{-3}{4}$ to a decimal or find a common denominator.
Using decimals:
$\frac{-3}{4} = -0.75$
The numbers we are comparing are $-0.75$ and $-2$.
On a number line, numbers increase from left to right. Negative numbers closer to 0 are larger than negative numbers farther from 0.
Since $-0.75$ is closer to 0 than $-2$, $-0.75$ is greater than $-2$.
$-0.75 > -2$
Substituting the original fraction back:
$\frac{-3}{4} > -2$
This shows that $\frac{-3}{4}$ is greater than –2, not smaller than –2.
Therefore, the statement "$\frac{-3}{4}$ is smaller than –2" is false.
Question 80. 0 is a rational number.
Answer:
True (T)
A rational number is defined as any number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q$ is not equal to zero ($q \neq 0$).
We need to determine if the number 0 can be written in this form.
Consider the fraction $\frac{0}{1}$. Here, the numerator $p = 0$, which is an integer. The denominator $q = 1$, which is also an integer and is not equal to zero ($1 \neq 0$).
Since 0 can be expressed as $\frac{0}{1}$ (or $\frac{0}{2}$, $\frac{0}{-5}$, etc.), where the numerator is an integer and the denominator is a non-zero integer, 0 fits the definition of a rational number.
Therefore, 0 is a rational number.
Question 81. All positive rational numbers lie between 0 and 1000.
Answer:
False (F)
The statement claims that every positive rational number is located on the number line strictly between 0 and 1000.
This means that for any positive rational number $x$, the inequality $0 < x < 1000$ should hold true.
A positive rational number is any rational number greater than 0. For example, $\frac{1}{2}$, $5$, $\frac{1001}{1}$, $\frac{3}{2}$ are all positive rational numbers.
Let's consider some examples:
- The rational number 5 is positive, and $0 < 5 < 1000$. This number lies between 0 and 1000.
- The rational number 500 is positive, and $0 < 500 < 1000$. This number lies between 0 and 1000.
However, consider the rational number 1500.
1500 is a positive number, and it is a rational number because it can be written as $\frac{1500}{1}$.
We need to check if it lies between 0 and 1000, i.e., if $0 < 1500 < 1000$.
The inequality $0 < 1500$ is true.
However, the inequality $1500 < 1000$ is false.
Since we found a positive rational number (1500) that does not lie between 0 and 1000, the statement "All positive rational numbers lie between 0 and 1000" is false.
There are infinitely many positive rational numbers greater than 1000 (e.g., 1001, $\frac{2001}{2}$, etc.).
Question 82. The population of India in 2004 - 05 is a rational number.
Answer:
True (T)
A rational number is a number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
The population of a country is the count of the number of people living in that country at a particular time. This count is always a whole number (a non-negative integer).
For example, the population of India in 2004-05 was a very large positive integer.
All integers are rational numbers because any integer $n$ can be written as a fraction $\frac{n}{1}$, where $n$ is an integer and $1$ is a non-zero integer.
Since the population of India in 2004-05 was a specific integer, and every integer is a rational number, the population of India in 2004-05 is a rational number.
Question 83. There are countless rational numbers between $\frac{5}{6}$ and $\frac{8}{9}$ .
Answer:
True (T)
The statement claims that there are countless rational numbers between $\frac{5}{6}$ and $\frac{8}{9}$. The term "countless" typically means infinitely many.
This relates to a fundamental property of rational numbers called density.
The property of density states that between any two distinct rational numbers, there exists at least one other rational number.
Let $r_1$ and $r_2$ be two distinct rational numbers, with $r_1 < r_2$. Their average, $\frac{r_1 + r_2}{2}$, is also a rational number and lies strictly between $r_1$ and $r_2$.
Since we can find one rational number between $r_1$ and $r_2$, we can then find another rational number between $r_1$ and that new number, and another between the new number and $r_2$. We can repeat this process infinitely many times, continuously finding new rational numbers within the interval $(r_1, r_2)$.
In this question, $\frac{5}{6}$ and $\frac{8}{9}$ are two distinct rational numbers. To confirm they are distinct and ordered, we can compare them:
Find a common denominator for 6 and 9, which is 18.
$\frac{5}{6} = \frac{5 \times 3}{6 \times 3} = \frac{15}{18}$
$\frac{8}{9} = \frac{8 \times 2}{9 \times 2} = \frac{16}{18}$
Since $\frac{15}{18} < \frac{16}{18}$, we have $\frac{5}{6} < \frac{8}{9}$. They are distinct rational numbers.
According to the density property of rational numbers, there are infinitely many rational numbers between $\frac{5}{6}$ and $\frac{8}{9}$.
Therefore, the statement "There are countless rational numbers between $\frac{5}{6}$ and $\frac{8}{9}$" is true.
Question 84. The reciprocal of x–1 is $\frac{1}{x}$ .
Answer:
False (F)
By the definition of negative exponents, $x^{-1} = \frac{1}{x}$ for any non-zero rational number $x$.
The reciprocal of a number is the value you multiply it by to get 1.
We need to find the reciprocal of $x^{-1}$ (which is $\frac{1}{x}$). Let the reciprocal be $y$. Then:
$x^{-1} \times y = 1$
Substitute $x^{-1} = \frac{1}{x}$:
$\frac{1}{x} \times y = 1$
Multiplying both sides by $x$ (assuming $x \neq 0$), we get:
$y = x$
So, the reciprocal of $x^{-1}$ is $x$.
The statement claims the reciprocal of $x^{-1}$ is $\frac{1}{x}$. This is only true if $x = \frac{1}{x}$, which means $x^2=1$, true only for $x=1$ or $x=-1$. It is not true for all non-zero rational numbers $x$.
Question 85. The rational number $\frac{57}{23}$ lies to the left of zero on the number line.
Answer:
False (F)
On the number line, positive numbers lie to the right of zero, and negative numbers lie to the left of zero.
A rational number $\frac{p}{q}$ is positive if the numerator $p$ and the denominator $q$ have the same sign.
The given rational number is $\frac{57}{23}$.
The numerator is 57, which is a positive integer ($57 > 0$).
The denominator is 23, which is also a positive integer ($23 > 0$).
Since both the numerator and the denominator are positive, the rational number $\frac{57}{23}$ is a positive number.
$\frac{57}{23} > 0$
As $\frac{57}{23}$ is a positive number, it lies to the right of zero on the number line.
Therefore, the statement that $\frac{57}{23}$ lies to the left of zero is false.
Question 86. The rational number $\frac{7}{-4}$ lies to the right of zero on the number line.
Answer:
False (F)
On the number line, numbers to the right of zero are positive numbers ($> 0$), and numbers to the left of zero are negative numbers ($< 0$).
We need to determine the sign of the rational number $\frac{7}{-4}$.
A rational number is positive if its numerator and denominator have the same sign (both positive or both negative). A rational number is negative if its numerator and denominator have different signs (one positive and one negative).
In the rational number $\frac{7}{-4}$:
The numerator is 7, which is a positive integer ($7 > 0$).
The denominator is –4, which is a negative integer ($-4 < 0$).
Since the numerator and the denominator have different signs (one positive and one negative), the rational number $\frac{7}{-4}$ is a negative number.
$\frac{7}{-4} < 0$
Negative numbers lie to the left of zero on the number line.
Therefore, the rational number $\frac{7}{-4}$ lies to the left of zero on the number line.
The statement claims that it lies to the right of zero, which is incorrect.
Question 87. The rational number $\frac{-8}{-3}$ lies neither to the right nor to the left of zero on the number line.
Answer:
False (F)
On the number line, numbers lie to the right of zero (positive numbers), to the left of zero (negative numbers), or exactly at zero (the number 0 itself).
A number lies neither to the right nor to the left of zero only if the number is zero.
We need to determine the value of the rational number $\frac{-8}{-3}$.
When both the numerator and the denominator of a fraction are negative, the fraction is equivalent to a positive fraction.
$\frac{-8}{-3} = \frac{-1 \times 8}{-1 \times 3} = \frac{8}{3}$
So the rational number is $\frac{8}{3}$.
Is $\frac{8}{3}$ equal to zero?
No, $\frac{8}{3} \neq 0$. Since $\frac{8}{3} = 2\frac{2}{3} = 2.66\dots$, it is a positive number.
$\frac{8}{3} > 0$
Positive numbers lie to the right of zero on the number line.
Therefore, the rational number $\frac{-8}{-3}$ (which is equal to $\frac{8}{3}$) lies to the right of zero on the number line.
The statement claims it lies neither to the right nor to the left of zero, which is false.
Question 88. The rational numbers $\frac{1}{2}$ and –1 are on the opposite sides of zero on the number line.
Answer:
True (T)
On the number line, the number zero is the point of origin. Positive numbers are located to the right of zero, and negative numbers are located to the left of zero.
We are given two rational numbers: $\frac{1}{2}$ and –1.
Let's determine the sign of each number:
- The number $\frac{1}{2}$ is a positive number. This means $\frac{1}{2} > 0$. Positive numbers lie to the right of zero on the number line.
- The number –1 is a negative number. This means $-1 < 0$. Negative numbers lie to the left of zero on the number line.
Since $\frac{1}{2}$ is positive and –1 is negative, they are on different sides of zero on the number line.
Therefore, the rational numbers $\frac{1}{2}$ and –1 are on the opposite sides of zero on the number line.
Question 89. Every fraction is a rational number.
Answer:
True (T)
A fraction is generally defined as a number expressed in the form $\frac{a}{b}$, where $a$ and $b$ are numbers and $b \neq 0$.
A rational number is defined as a number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
The statement claims that every fraction is a rational number. Let's consider a typical fraction $\frac{a}{b}$.
For this fraction to be a rational number, the numerator $a$ must be an integer and the denominator $b$ must be a non-zero integer.
In the context of elementary mathematics where this statement is usually encountered, "fraction" almost always refers to fractions where the numerator and denominator are integers.
For example, $\frac{1}{2}$, $\frac{3}{4}$, $\frac{-5}{7}$, $\frac{6}{-1}$ are all fractions where the numerator and denominator are integers, and the denominator is non-zero. These all fit the definition of rational numbers.
While in more advanced contexts, fractions can involve other types of numbers (like $\frac{\sqrt{2}}{3}$ or $\frac{\pi}{2}$), the standard definition of a fraction in arithmetic aligns with the requirements for a rational number.
Assuming the standard definition where the numerator and denominator of a fraction are integers, every fraction $\frac{a}{b}$ with $b \neq 0$ has $a$ as an integer and $b$ as a non-zero integer. This fits the definition of a rational number.
Therefore, every fraction (in the standard sense with integer numerator and denominator) is a rational number.
Question 90. Every integer is a rational number.
Answer:
True (T)
A rational number is defined as any number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q$ is not equal to zero ($q \neq 0$).
An integer is a whole number (positive, negative, or zero). The set of integers includes $\dots, -3, -2, -1, 0, 1, 2, 3, \dots$.
We need to determine if every integer can be written in the form $\frac{p}{q}$ where $p$ and $q$ are integers and $q \neq 0$.
Consider any integer, let's call it $n$. We can always express any integer $n$ as a fraction by setting the denominator to 1:
$n = \frac{n}{1}$
In this fraction $\frac{n}{1}$, the numerator is $n$, which is an integer. The denominator is 1, which is also an integer and is not equal to zero ($1 \neq 0$).
Since any integer $n$ can be written in the form $\frac{p}{q}$ where $p=n$ (an integer) and $q=1$ (a non-zero integer), every integer fits the definition of a rational number.
Therefore, every integer is a rational number.
Question 91. The rational numbers can be represented on the number line.
Answer:
True (T)
The number line is a graphical representation where every point corresponds to a unique real number.
A rational number is a number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
To represent a rational number $\frac{p}{q}$ on the number line:
- First, locate the integer part of the rational number. For example, for $\frac{7}{3} = 2\frac{1}{3}$, the integer part is 2. For $-\frac{5}{4} = -1\frac{1}{4}$, the integer part is -1.
- Consider the segment between this integer and the next integer (e.g., between 2 and 3 for $\frac{7}{3}$, or between -1 and -2 for $-\frac{5}{4}$).
- Divide this segment into $|q|$ equal parts.
- Count $|p|$ of these parts starting from the integer part. Move to the right if the number is positive, and to the left if the number is negative.
Since every rational number can be written in the form $\frac{p}{q}$, and this method allows us to locate a specific point on the number line for any such fraction, every rational number can be represented on the number line.
Question 92. The negative of a negative rational number is a positive rational number.
Answer:
True (T)
Let $x$ be a negative rational number.
By definition, a negative number is a number that is less than zero. So, $x < 0$.
The negative of a number $x$ is denoted by $-x$. It is also known as the additive inverse of $x$, because $x + (-x) = 0$.
The statement asks about "the negative of a negative rational number". This means we need to consider the negative of the number $x$, where $x$ itself is a negative rational number.
So, we are interested in the value of $-x$.
Since $x$ is a negative number, we can write $x = -k$ for some positive rational number $k$ (i.e., $k > 0$).
Then, the negative of $x$ is:
$-x = -(-k)$
Using the property that the negative of a negative is the original number, we have:
$-(-k) = k$
So, $-x = k$.
Since $k$ is a positive rational number, $-x$ is a positive rational number.
Alternatively, we can use the property of inequalities. Given $x < 0$, if we multiply both sides of the inequality by $-1$, we reverse the inequality sign:
$(-1) \times x > (-1) \times 0$
$-x > 0$
Since $-x > 0$, $-x$ is a positive number. As $x$ is rational, $-x$ is also rational.
Thus, the negative of a negative rational number is indeed a positive rational number.
For example, the negative of $-\frac{2}{3}$ is $- (-\frac{2}{3}) = \frac{2}{3}$, which is a positive rational number.
Question 93. If x and y are two rational numbers such that x > y, then x – y is always a positive rational number.
Answer:
True (T)
Let $x$ and $y$ be two rational numbers such that $x > y$.
We want to determine the sign of the difference $x - y$.
Consider the given inequality:
$x > y$
Subtract $y$ from both sides of the inequality. Subtracting the same number from both sides of an inequality does not change the direction of the inequality:
$x - y > y - y$
Simplifying the right side:
$x - y > 0$
The inequality $x - y > 0$ means that the difference $x - y$ is a positive number.
Also, the set of rational numbers is closed under subtraction, meaning that the difference of any two rational numbers is always a rational number.
Since $x$ and $y$ are rational numbers, $x - y$ is a rational number. Since $x - y > 0$, it is a positive rational number.
Therefore, if $x$ and $y$ are rational numbers such that $x > y$, their difference $x - y$ is always a positive rational number.
Question 94. 0 is the smallest rational number.
Answer:
False (F)
The statement claims that 0 is the smallest rational number.
The set of rational numbers includes positive numbers, negative numbers, and zero.
On the number line, numbers decrease as you move to the left.
Consider any negative rational number, for instance, –1. –1 is a rational number (it can be written as $\frac{-1}{1}$).
Comparing –1 and 0, we see that $-1 < 0$. This means –1 is smaller than 0.
We can take even smaller rational numbers, such as –10, –100, or $-\frac{1}{2}$. All of these are rational numbers, and they are all smaller than 0.
For any given negative rational number $r$, we can always find a smaller rational number, for example, $r - 1$ or $2r$ (if $r$ is negative, $2r$ will be twice as far from zero in the negative direction, hence smaller). This means there is no smallest negative rational number.
Since there are negative rational numbers, and any negative number is smaller than 0, 0 cannot be the smallest rational number.
Therefore, the statement "0 is the smallest rational number" is false.
Question 95. Every whole number is an integer.
Answer:
True (T)
The set of whole numbers consists of zero and the natural (counting) numbers. The set of whole numbers is usually denoted by $W$ and is $\{0, 1, 2, 3, 4, \dots\}$.
The set of integers consists of positive whole numbers, negative whole numbers, and zero. The set of integers is usually denoted by $Z$ or $\mathbb{Z}$ and is $\{\dots, -3, -2, -1, 0, 1, 2, 3, \dots\}$.
The statement claims that every whole number is an integer.
Let's look at the elements in the set of whole numbers: 0, 1, 2, 3, 4, ...
Now let's look at the elements in the set of integers: ..., -3, -2, -1, 0, 1, 2, 3, ...
We can see that every number in the set of whole numbers $\{0, 1, 2, 3, \dots\}$ is also present in the set of integers $\{\dots, -3, -2, -1, 0, 1, 2, 3, \dots\}$.
The set of whole numbers is a subset of the set of integers.
Therefore, every whole number is an integer.
Question 96. Every whole number is a rational number.
Answer:
True (T)
A whole number is any number from the set $\{0, 1, 2, 3, \dots\}$.
A rational number is any number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
We need to determine if every whole number can be written in the form $\frac{p}{q}$ where $p$ and $q$ are integers and $q \neq 0$.
Let $w$ be any whole number. Since whole numbers are a subset of integers, $w$ is also an integer.
As we established in Question 90, every integer can be written as a rational number by expressing it as a fraction with a denominator of 1.
For any whole number $w$, we can write:
$w = \frac{w}{1}$
In this fraction $\frac{w}{1}$, the numerator is $w$, which is an integer. The denominator is 1, which is also an integer and is not equal to zero ($1 \neq 0$).
Since any whole number $w$ can be written in the form $\frac{p}{q}$ where $p=w$ (an integer) and $q=1$ (a non-zero integer), every whole number fits the definition of a rational number.
Therefore, every whole number is a rational number.
Question 97. 0 is whole number but it is not a rational number.
Answer:
False (F)
The statement consists of two parts connected by "but":
- "0 is a whole number"
- "it is not a rational number"
For the entire statement to be true, both parts must be true.
Part 1: Is 0 a whole number?
The set of whole numbers is $\{0, 1, 2, 3, \dots\}$. Yes, 0 is included in the set of whole numbers.
This part of the statement is True.
Part 2: Is 0 not a rational number?
A rational number is defined as a number that can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
We can write 0 as a fraction $\frac{0}{1}$. Here, the numerator $p = 0$ is an integer, and the denominator $q = 1$ is a non-zero integer.
Since 0 can be expressed in the form $\frac{p}{q}$ where $p$ and $q$ are integers and $q \neq 0$, 0 fits the definition of a rational number.
So, 0 is a rational number.
This part of the statement ("it is not a rational number") is False.
Since the second part of the statement is false, the entire combined statement "0 is a whole number but it is not a rational number" is false.
Question 98. The rational numbers $\frac{1}{2}$ and $-\frac{5}{2}$ are on the opposite sides of 0 on the number line.
Answer:
True (T)
On the number line, the number zero serves as the dividing point between positive and negative numbers.
Numbers located to the right of zero are positive numbers, and numbers located to the left of zero are negative numbers.
For two numbers to be on opposite sides of zero, one must be positive and the other must be negative (assuming neither is zero itself).
Let's examine the signs of the given rational numbers:
- The first number is $\frac{1}{2}$. The numerator (1) is positive, and the denominator (2) is positive. A rational number with a positive numerator and a positive denominator is positive. So, $\frac{1}{2} > 0$. This number is located to the right of 0.
- The second number is $-\frac{5}{2}$. This number can be written as $\frac{-5}{2}$. The numerator (–5) is negative, and the denominator (2) is positive. A rational number with a negative numerator and a positive denominator is negative. So, $-\frac{5}{2} < 0$. This number is located to the left of 0.
Since $\frac{1}{2}$ is a positive number and $-\frac{5}{2}$ is a negative number, they are located on opposite sides of zero on the number line.
Therefore, the statement is true.
Question 99. Rational numbers can be added (or multiplied) in any order
$\frac{-4}{5}$ × $\frac{-6}{5}$ = $\frac{-6}{5}$ × $\frac{-4}{5}$
Answer:
True (T)
The statement consists of two parts. The first part is a general statement about the properties of addition and multiplication of rational numbers: "Rational numbers can be added (or multiplied) in any order". The second part is a specific example illustrating this property for multiplication: $\frac{-4}{5} \times \frac{-6}{5} = \frac{-6}{5} \times \frac{-4}{5}$.
The ability to add or multiply numbers in any order is known as the commutative property.
The commutative property for addition states that for any two rational numbers $a$ and $b$, $a + b = b + a$.
The commutative property for multiplication states that for any two rational numbers $a$ and $b$, $a \times b = b \times a$.
Rational numbers indeed satisfy both the commutative property of addition and the commutative property of multiplication.
The first part of the statement is therefore true.
The example provided, $\frac{-4}{5} \times \frac{-6}{5} = \frac{-6}{5} \times \frac{-4}{5}$, is a direct application of the commutative property of multiplication where $a = \frac{-4}{5}$ and $b = \frac{-6}{5}$.
Let's verify the equality in the example:
Left Hand Side (LHS): $\frac{-4}{5} \times \frac{-6}{5} = \frac{(-4) \times (-6)}{5 \times 5} = \frac{24}{25}$
Right Hand Side (RHS): $\frac{-6}{5} \times \frac{-4}{5} = \frac{(-6) \times (-4)}{5 \times 5} = \frac{24}{25}$
Since LHS = RHS, the example is correct and demonstrates the commutative property of multiplication for these specific rational numbers.
Because rational numbers are commutative under both addition and multiplication, the general statement is true.
Question 100 to 152
Question 100. Solve the following: Select the rational numbers from the list which are also the integers.
$\frac{9}{4}$ , $\frac{8}{4}$ , $\frac{7}{4}$ , $\frac{6}{4}$ , $\frac{9}{3}$ , $\frac{8}{3}$ , $\frac{7}{3}$ , $\frac{6}{3}$ , $\frac{5}{2}$ , $\frac{4}{2}$ , $\frac{3}{1}$ , $\frac{3}{2}$ , $\frac{1}{1}$ , $\frac{0}{1}$ , $\frac{-1}{1}$ , $\frac{-2}{1}$ , $\frac{-3}{2}$ , $\frac{-4}{2}$ , $\frac{-5}{2}$ , $\frac{-6}{2}$
Answer:
Solution:
A rational number is an integer if its denominator divides the numerator evenly, resulting in a whole number (positive, negative, or zero).
We check each number in the list:
$\frac{9}{4}$ (Not an integer)
$\frac{8}{4} = 2$ (Integer)
$\frac{7}{4}$ (Not an integer)
$\frac{6}{4} = \frac{3}{2}$ (Not an integer)
$\frac{9}{3} = 3$ (Integer)
$\frac{8}{3}$ (Not an integer)
$\frac{7}{3}$ (Not an integer)
$\frac{6}{3} = 2$ (Integer)
$\frac{5}{2}$ (Not an integer)
$\frac{4}{2} = 2$ (Integer)
$\frac{3}{1} = 3$ (Integer)
$\frac{3}{2}$ (Not an integer)
$\frac{1}{1} = 1$ (Integer)
$\frac{0}{1} = 0$ (Integer)
$\frac{-1}{1} = -1$ (Integer)
$\frac{-2}{1} = -2$ (Integer)
$\frac{-3}{2}$ (Not an integer)
$\frac{-4}{2} = -2$ (Integer)
$\frac{-5}{2}$ (Not an integer)
$\frac{-6}{2} = -3$ (Integer)
Answer:
The rational numbers from the list which are also integers are:
$\frac{8}{4}$, $\frac{9}{3}$, $\frac{6}{3}$, $\frac{4}{2}$, $\frac{3}{1}$, $\frac{1}{1}$, $\frac{0}{1}$, $\frac{-1}{1}$, $\frac{-2}{1}$, $\frac{-4}{2}$, $\frac{-6}{2}$.
Question 101. Select those which can be written as a rational number with denominator 4 in their lowest form:
$\frac{7}{8}$ , $\frac{64}{16}$ , $\frac{36}{-12}$ , $\frac{-16}{17}$ , $\frac{5}{-4}$ , $\frac{140}{28}$
Answer:
Given:
A list of rational numbers: $\frac{7}{8}$, $\frac{64}{16}$, $\frac{36}{-12}$, $\frac{-16}{17}$, $\frac{5}{-4}$, $\frac{140}{28}$.
To Find:
The numbers from the given list that can be written as a rational number with denominator 4 in their lowest form.
Solution:
To find the numbers that satisfy the condition, we need to simplify each fraction to its lowest form and then check if the denominator of the lowest form is 4.
1. For $\frac{7}{8}$:
The fraction $\frac{7}{8}$ is already in its lowest form as the greatest common divisor of 7 and 8 is 1. The denominator is 8, which is not 4.
2. For $\frac{64}{16}$:
Simplify the fraction:
$\frac{64}{16} = \frac{\cancel{64}^{4}}{\cancel{16}_{1}} = 4$
[Simplifying the fraction]
This can be written as $\frac{4}{1}$. The lowest form is 4, which is an integer. The denominator in lowest form is 1, not 4.
3. For $\frac{36}{-12}$:
Simplify the fraction:
$\frac{36}{-12} = -\frac{\cancel{36}^{3}}{\cancel{12}_{1}} = -3$
[Simplifying the fraction]
This can be written as $\frac{-3}{1}$. The lowest form is -3, which is an integer. The denominator in lowest form is 1, not 4.
4. For $\frac{-16}{17}$:
The fraction $\frac{-16}{17}$ is already in its lowest form as the greatest common divisor of 16 and 17 is 1. The denominator is 17, which is not 4.
5. For $\frac{5}{-4}$:
The fraction $\frac{5}{-4}$ is equivalent to $\frac{-5}{4}$. This fraction is already in its lowest form as the greatest common divisor of 5 and 4 is 1. The denominator is 4. This number satisfies the condition.
6. For $\frac{140}{28}$:
Simplify the fraction:
$\frac{140}{28} = \frac{\cancel{140}^{5}}{\cancel{28}_{1}} = 5$
[Simplifying the fraction]
This can be written as $\frac{5}{1}$. The lowest form is 5, which is an integer. The denominator in lowest form is 1, not 4.
Based on the simplification, only $\frac{5}{-4}$ results in a rational number with a denominator of 4 in its lowest form.
Answer:
The rational number from the list which can be written as a rational number with denominator 4 in its lowest form is:
$\frac{5}{-4}$
Question 102. Using suitable rearrangement and find the sum:
(a) $\frac{4}{7}$ + $\left( \frac{-4}{9} \right)$ + $\frac{3}{7}$ + $\left( \frac{-13}{9} \right)$
(b) -5 + $\frac{7}{10}$ + $\frac{3}{7}$ + (-3) + $\frac{5}{14}$ + $\frac{-4}{5}$
Answer:
Solution (a):
We need to find the sum of $\frac{4}{7} + \left( \frac{-4}{9} \right) + \frac{3}{7} + \left( \frac{-13}{9} \right)$.
Rearrange the terms to group those with the same denominator:
$\left( \frac{4}{7} + \frac{3}{7} \right) + \left( \frac{-4}{9} + \frac{-13}{9} \right)$
Add the fractions within each group:
$\frac{4+3}{7} + \frac{-4+(-13)}{9}$
$\frac{7}{7} + \frac{-4-13}{9}$
Simplify the fractions:
$\frac{7}{7} = 1$
[Simplifying the first fraction]
$\frac{-17}{9}$
[Simplifying the second fraction]
Now, add the simplified results:
$1 + \left( \frac{-17}{9} \right) = 1 - \frac{17}{9}$
To subtract, find a common denominator, which is 9:
$\frac{9}{9} - \frac{17}{9} = \frac{9-17}{9}$
$\frac{-8}{9}$
Answer (a):
The sum is $\frac{-8}{9}$.
Solution (b):
We need to find the sum of $-5 + \frac{7}{10} + \frac{3}{7} + (-3) + \frac{5}{14} + \frac{-4}{5}$.
Rearrange the terms to group integers and fractions with potentially related denominators:
$(-5 + (-3)) + \left( \frac{7}{10} + \frac{-4}{5} \right) + \left( \frac{3}{7} + \frac{5}{14} \right)$
Sum the integers:
[Sum of integers]
Sum the fractions in the first group ($\frac{7}{10}$ and $\frac{-4}{5}$). The common denominator for 10 and 5 is 10:
$\frac{7}{10} + \frac{-4 \times 2}{5 \times 2} = \frac{7}{10} + \frac{-8}{10} = \frac{7+(-8)}{10} = \frac{-1}{10}$
Sum the fractions in the second group ($\frac{3}{7}$ and $\frac{5}{14}$). The common denominator for 7 and 14 is 14:
$\frac{3 \times 2}{7 \times 2} + \frac{5}{14} = \frac{6}{14} + \frac{5}{14} = \frac{6+5}{14} = \frac{11}{14}$
Now, add the sums of the groups:
$-8 + \left( \frac{-1}{10} \right) + \frac{11}{14}$
To add $\frac{-1}{10}$ and $\frac{11}{14}$, find the least common multiple (LCM) of 10 and 14.
Prime factorization of 10 is $2 \times 5$.
Prime factorization of 14 is $2 \times 7$.
LCM(10, 14) = $2 \times 5 \times 7 = 70$.
Convert the fractions to have a denominator of 70:
$\frac{-1}{10} = \frac{-1 \times 7}{10 \times 7} = \frac{-7}{70}$
$\frac{11}{14} = \frac{11 \times 5}{14 \times 5} = \frac{55}{70}$
Now add the integers and the fractions:
$-8 + \left( \frac{-7}{70} + \frac{55}{70} \right)$
$-8 + \frac{-7+55}{70}$
$-8 + \frac{48}{70}$
Simplify the fraction $\frac{48}{70}$ by dividing both numerator and denominator by their greatest common divisor, which is 2:
$\frac{\cancel{48}^{24}}{\cancel{70}_{35}} = \frac{24}{35}$
[Simplifying the fraction]
So the expression becomes:
$-8 + \frac{24}{35}$
Convert -8 into a fraction with denominator 35:
$-8 = \frac{-8 \times 35}{1 \times 35} = \frac{-280}{35}$
Now add the fractions:
$\frac{-280}{35} + \frac{24}{35} = \frac{-280 + 24}{35}$
$\frac{-256}{35}$
Answer (b):
The sum is $\frac{-256}{35}$.
Question 103. Verify – (– x) = x for
(i) x = $\frac{3}{5}$
(ii) x = $\frac{-7}{9}$
(iii) x = $\frac{13}{-15}$
Answer:
We need to verify that $-(-x) = x$ for the given values of $x$.
(i) Verify for $x = \frac{3}{5}$
Given $x = \frac{3}{5}$.
First, find $-x$:
$-x = -\left( \frac{3}{5} \right) = \frac{-3}{5}$
Now, find $-(-x)$:
$-(-x) = -\left( \frac{-3}{5} \right)$
The negative of a negative number is positive:
$- \left( \frac{-3}{5} \right) = \frac{3}{5}$
We see that $-(-x) = \frac{3}{5}$, which is equal to the original value of $x$.
Thus, $-(-x) = x$ is verified for $x = \frac{3}{5}$.
(ii) Verify for $x = \frac{-7}{9}$
Given $x = \frac{-7}{9}$.
First, find $-x$:
$-x = -\left( \frac{-7}{9} \right)$
The negative of a negative number is positive:
$- \left( \frac{-7}{9} \right) = \frac{7}{9}$
Now, find $-(-x)$:
$-(-x) = -\left( \frac{7}{9} \right) = \frac{-7}{9}$
We see that $-(-x) = \frac{-7}{9}$, which is equal to the original value of $x$.
Thus, $-(-x) = x$ is verified for $x = \frac{-7}{9}$.
(iii) Verify for $x = \frac{13}{-15}$
Given $x = \frac{13}{-15}$. Note that $\frac{13}{-15}$ is equivalent to $\frac{-13}{15}$. So, $x = \frac{-13}{15}$.
First, find $-x$:
$-x = -\left( \frac{-13}{15} \right)$
The negative of a negative number is positive:
$- \left( \frac{-13}{15} \right) = \frac{13}{15}$
Now, find $-(-x)$:
$-(-x) = -\left( \frac{13}{15} \right) = \frac{-13}{15}$
We see that $-(-x) = \frac{-13}{15}$, which is equal to the original value of $x$ (since $\frac{13}{-15} = \frac{-13}{15}$).
Thus, $-(-x) = x$ is verified for $x = \frac{13}{-15}$.
Question 104. Give one example each to show that the rational numbers are closed under addition, subtraction and multiplication. Are rational numbers closed under division? Give two examples in support of your answer.
Answer:
The property of closure states that if an operation is performed on any two elements of a set, the result is also an element of that set.
Closure under Addition:
Let $a = \frac{1}{2}$ and $b = \frac{1}{3}$ be two rational numbers.
Their sum is $a+b = \frac{1}{2} + \frac{1}{3}$.
To add these fractions, find a common denominator (LCM of 2 and 3 is 6):
$a+b = \frac{1 \times 3}{2 \times 3} + \frac{1 \times 2}{3 \times 2} = \frac{3}{6} + \frac{2}{6} = \frac{3+2}{6} = \frac{5}{6}$.
The result $\frac{5}{6}$ is a rational number (since 5 and 6 are integers and $6 \neq 0$).
This example shows that the sum of two rational numbers is a rational number. Rational numbers are closed under addition.
Closure under Subtraction:
Let $a = \frac{3}{4}$ and $b = \frac{1}{4}$ be two rational numbers.
Their difference is $a-b = \frac{3}{4} - \frac{1}{4}$.
Since they have the same denominator, we subtract the numerators:
$a-b = \frac{3-1}{4} = \frac{2}{4}$.
Simplify the fraction:
$\frac{\cancel{2}^{1}}{\cancel{4}_{2}} = \frac{1}{2}$
[Simplifying the fraction]
The result $\frac{1}{2}$ is a rational number (since 1 and 2 are integers and $2 \neq 0$).
This example shows that the difference of two rational numbers is a rational number. Rational numbers are closed under subtraction.
Closure under Multiplication:
Let $a = \frac{2}{3}$ and $b = \frac{3}{5}$ be two rational numbers.
Their product is $a \times b = \frac{2}{3} \times \frac{3}{5}$.
Multiply the numerators and the denominators:
$a \times b = \frac{2 \times 3}{3 \times 5} = \frac{6}{15}$.
Simplify the fraction:
$\frac{\cancel{6}^{2}}{\cancel{15}_{5}} = \frac{2}{5}$
[Simplifying the fraction]
The result $\frac{2}{5}$ is a rational number (since 2 and 5 are integers and $5 \neq 0$).
This example shows that the product of two rational numbers is a rational number. Rational numbers are closed under multiplication.
Closure under Division:
Are rational numbers closed under division?
Consider division of a rational number $a$ by a rational number $b$ ($a \div b$ or $\frac{a}{b}$). For the result to be a rational number, it must be possible to express $\frac{a}{b}$ in the form $\frac{p}{q}$ where $p, q$ are integers and $q \neq 0$.
Let's consider two examples:
Example 1: Let $a = \frac{1}{2}$ and $b = \frac{1}{4}$ be two rational numbers, where $b \neq 0$.
Their quotient is $a \div b = \frac{1}{2} \div \frac{1}{4} = \frac{1}{2} \times \frac{4}{1} = \frac{1 \times 4}{2 \times 1} = \frac{4}{2} = 2$.
The result 2 can be written as $\frac{2}{1}$, which is a rational number.
Example 2: Let $a = \frac{1}{2}$ and $b = 0$ be two rational numbers. Note that 0 can be written as $\frac{0}{1}$, which is a rational number.
Their quotient is $a \div b = \frac{1}{2} \div 0$.
Division by zero is undefined. The result is not a rational number (it is not a number at all in the standard number system).
Since division by zero (where the divisor is a rational number, 0) does not result in a rational number, the set of rational numbers is not closed under division.
Conclusion:
Rational numbers are closed under addition, subtraction, and multiplication. However, they are not closed under division because division by the rational number 0 is undefined.
Question 105. Verify the property x + y = y + x of rational numbers by taking
(a) x = $\frac{1}{2}$ , y = $\frac{1}{2}$
(b) x = $\frac{-2}{3}$ , y = $\frac{-5}{6}$
(c) x = $\frac{-3}{7}$ , y = $\frac{20}{21}$
(d) x = $\frac{-2}{5}$ , y = $\frac{-9}{10}$
Answer:
We need to verify the commutative property of addition, $x + y = y + x$, for the given pairs of rational numbers.
(a) Verify for $x = \frac{1}{2}$, $y = \frac{1}{2}$
LHS: $x + y = \frac{1}{2} + \frac{1}{2}$
$x + y = \frac{1+1}{2} = \frac{2}{2} = 1$
RHS: $y + x = \frac{1}{2} + \frac{1}{2}$
$y + x = \frac{1+1}{2} = \frac{2}{2} = 1$
Since LHS = RHS ($1 = 1$), the property $x + y = y + x$ is verified for $x = \frac{1}{2}$ and $y = \frac{1}{2}$.
(b) Verify for $x = \frac{-2}{3}$, $y = \frac{-5}{6}$
LHS: $x + y = \frac{-2}{3} + \left( \frac{-5}{6} \right) = \frac{-2}{3} - \frac{5}{6}$
Find a common denominator for 3 and 6, which is 6:
$x + y = \frac{-2 \times 2}{3 \times 2} - \frac{5}{6} = \frac{-4}{6} - \frac{5}{6} = \frac{-4 - 5}{6} = \frac{-9}{6}$
Simplify the fraction:
$\frac{-9}{6} = \frac{\cancel{-9}^{-3}}{\cancel{6}_{2}} = \frac{-3}{2}$
[Simplifying LHS]
RHS: $y + x = \frac{-5}{6} + \left( \frac{-2}{3} \right) = \frac{-5}{6} - \frac{2}{3}$
Find a common denominator for 6 and 3, which is 6:
$y + x = \frac{-5}{6} - \frac{2 \times 2}{3 \times 2} = \frac{-5}{6} - \frac{4}{6} = \frac{-5 - 4}{6} = \frac{-9}{6}$
Simplify the fraction:
$\frac{-9}{6} = \frac{\cancel{-9}^{-3}}{\cancel{6}_{2}} = \frac{-3}{2}$
[Simplifying RHS]
Since LHS = RHS ($\frac{-3}{2} = \frac{-3}{2}$), the property $x + y = y + x$ is verified for $x = \frac{-2}{3}$ and $y = \frac{-5}{6}$.
(c) Verify for $x = \frac{-3}{7}$, $y = \frac{20}{21}$
LHS: $x + y = \frac{-3}{7} + \frac{20}{21}$
Find a common denominator for 7 and 21, which is 21:
$x + y = \frac{-3 \times 3}{7 \times 3} + \frac{20}{21} = \frac{-9}{21} + \frac{20}{21} = \frac{-9 + 20}{21} = \frac{11}{21}$
RHS: $y + x = \frac{20}{21} + \left( \frac{-3}{7} \right) = \frac{20}{21} - \frac{3}{7}$
Find a common denominator for 21 and 7, which is 21:
$y + x = \frac{20}{21} - \frac{3 \times 3}{7 \times 3} = \frac{20}{21} - \frac{9}{21} = \frac{20 - 9}{21} = \frac{11}{21}$
Since LHS = RHS ($\frac{11}{21} = \frac{11}{21}$), the property $x + y = y + x$ is verified for $x = \frac{-3}{7}$ and $y = \frac{20}{21}$.
(d) Verify for $x = \frac{-2}{5}$, $y = \frac{-9}{10}$
LHS: $x + y = \frac{-2}{5} + \left( \frac{-9}{10} \right) = \frac{-2}{5} - \frac{9}{10}$
Find a common denominator for 5 and 10, which is 10:
$x + y = \frac{-2 \times 2}{5 \times 2} - \frac{9}{10} = \frac{-4}{10} - \frac{9}{10} = \frac{-4 - 9}{10} = \frac{-13}{10}$
RHS: $y + x = \frac{-9}{10} + \left( \frac{-2}{5} \right) = \frac{-9}{10} - \frac{2}{5}$
Find a common denominator for 10 and 5, which is 10:
$y + x = \frac{-9}{10} - \frac{2 \times 2}{5 \times 2} = \frac{-9}{10} - \frac{4}{10} = \frac{-9 - 4}{10} = \frac{-13}{10}$
Since LHS = RHS ($\frac{-13}{10} = \frac{-13}{10}$), the property $x + y = y + x$ is verified for $x = \frac{-2}{5}$ and $y = \frac{-9}{10}$.
Question 106. Simplify each of the following by using suitable property. Also name the property.
(a) $\left[ \frac{1}{2}\times\frac{1}{4} \right]$ + $\left[ \frac{1}{2}\times 6 \right]$
(b) $\left[ \frac{1}{5}\times\frac{2}{15} \right]$ - $\left[ \frac{1}{5}\times\frac{2}{15} \right]$
(c) $\frac{-3}{5}$ × $\left\{ \frac{3}{7}+\left( \frac{-5}{6} \right) \right\}$
Answer:
(a) Simplify $\left[ \frac{1}{2}\times\frac{1}{4} \right]$ + $\left[ \frac{1}{2}\times 6 \right]$
Notice that $\frac{1}{2}$ is a common factor in both terms. We can use the distributive property of multiplication over addition, which states that $a \times b + a \times c = a \times (b + c)$.
Here, $a = \frac{1}{2}$, $b = \frac{1}{4}$, and $c = 6$.
So, $\left[ \frac{1}{2}\times\frac{1}{4} \right]$ + $\left[ \frac{1}{2}\times 6 \right] = \frac{1}{2} \times \left( \frac{1}{4} + 6 \right)$
First, calculate the sum inside the parentheses:
$\frac{1}{4} + 6 = \frac{1}{4} + \frac{6 \times 4}{1 \times 4} = \frac{1}{4} + \frac{24}{4} = \frac{1+24}{4} = \frac{25}{4}$
Now, multiply the result by $\frac{1}{2}$:
$\frac{1}{2} \times \frac{25}{4} = \frac{1 \times 25}{2 \times 4} = \frac{25}{8}$
Property Used (a): Distributive property of multiplication over addition.
Answer (a): $\frac{25}{8}$
(b) Simplify $\left[ \frac{1}{5}\times\frac{2}{15} \right]$ - $\left[ \frac{1}{5}\times\frac{2}{15} \right]$
Let $P = \frac{1}{5}\times\frac{2}{15}$. The expression is in the form $P - P$. Any quantity subtracted from itself is 0.
Let's first calculate the value of $P$:
$P = \frac{1}{5}\times\frac{2}{15} = \frac{1 \times 2}{5 \times 15} = \frac{2}{75}$
So the expression becomes:
$\frac{2}{75} - \frac{2}{75} = 0$
The property used here is the fact that subtracting a number from itself results in 0. This is related to the additive inverse property ($a + (-a) = 0$), where $a - a = a + (-a) = 0$.
Property Used (b): Additive inverse property (or simply the property that $x - x = 0$).
Answer (b): $0$
(c) Simplify $\frac{-3}{5}$ × $\left\{ \frac{3}{7}+\left( \frac{-5}{6} \right) \right\}$
The expression is in the form $a \times (b + c)$. We can use the distributive property of multiplication over addition, which states that $a \times (b + c) = a \times b + a \times c$.
Here, $a = \frac{-3}{5}$, $b = \frac{3}{7}$, and $c = \frac{-5}{6}$.
Distribute $\frac{-3}{5}$:
$\frac{-3}{5} \times \left( \frac{3}{7} + \frac{-5}{6} \right) = \left( \frac{-3}{5} \times \frac{3}{7} \right) + \left( \frac{-3}{5} \times \frac{-5}{6} \right)$
Calculate the products:
$\frac{-3}{5} \times \frac{3}{7} = \frac{-3 \times 3}{5 \times 7} = \frac{-9}{35}$
$\frac{-3}{5} \times \frac{-5}{6} = \frac{(-3) \times (-5)}{5 \times 6} = \frac{15}{30}$
Simplify the second fraction:
$\frac{15}{30} = \frac{\cancel{15}^{1}}{\cancel{30}_{2}} = \frac{1}{2}$
[Simplifying the product]
Now, add the two results:
$\frac{-9}{35} + \frac{1}{2}$
Find a common denominator for 35 and 2, which is LCM(35, 2) = $35 \times 2 = 70$ (since they are coprime).
$\frac{-9 \times 2}{35 \times 2} + \frac{1 \times 35}{2 \times 35} = \frac{-18}{70} + \frac{35}{70}$
Add the numerators:
$\frac{-18 + 35}{70} = \frac{17}{70}$
Property Used (c): Distributive property of multiplication over addition.
Answer (c): $\frac{17}{70}$
Question 107. Tell which property allows you to compute
$\frac{1}{5}$ × $\left[ \frac{5}{6}\times\frac{7}{9} \right]$ as $\left[ \frac{1}{5}\times\frac{5}{6} \right]$ × $\frac{7}{9}$
Answer:
The given expression is of the form $a \times (b \times c) = (a \times b) \times c$, where $a = \frac{1}{5}$, $b = \frac{5}{6}$, and $c = \frac{7}{9}$.
This property states that when multiplying three or more numbers, the way the numbers are grouped does not affect the product.
This property is known as the Associative Property of Multiplication.
Answer:
The property that allows you to compute $\frac{1}{5}$ × $\left[ \frac{5}{6}\times\frac{7}{9} \right]$ as $\left[ \frac{1}{5}\times\frac{5}{6} \right]$ × $\frac{7}{9}$ is the Associative Property of Multiplication.
Question 108. Verify the property x × y = y × z of rational numbers by using
(a) x = 7 and y = $\frac{1}{2}$
(b) x = $\frac{2}{3}$ and y = $\frac{9}{4}$
(c) x = $\frac{-5}{7}$ and y = $\frac{14}{15}$
(d) x = $\frac{-3}{8}$ and y = $\frac{-4}{9}$
Answer:
We need to verify the commutative property of multiplication, $x \times y = y \times x$, for the given pairs of rational numbers.
(a) Verify for $x = 7$, $y = \frac{1}{2}$
LHS: $x \times y = 7 \times \frac{1}{2}$
$x \times y = \frac{7}{1} \times \frac{1}{2} = \frac{7 \times 1}{1 \times 2} = \frac{7}{2}$
RHS: $y \times x = \frac{1}{2} \times 7$
$y \times x = \frac{1}{2} \times \frac{7}{1} = \frac{1 \times 7}{2 \times 1} = \frac{7}{2}$
Since LHS = RHS ($\frac{7}{2} = \frac{7}{2}$), the property $x \times y = y \times x$ is verified for $x = 7$ and $y = \frac{1}{2}$.
(b) Verify for $x = \frac{2}{3}$, $y = \frac{9}{4}$
LHS: $x \times y = \frac{2}{3} \times \frac{9}{4}$
$x \times y = \frac{\cancel{2}^{1}}{\cancel{3}_{1}} \times \frac{\cancel{9}^{3}}{\cancel{4}_{2}} = \frac{1 \times 3}{1 \times 2} = \frac{3}{2}$
$\frac{2}{3} \times \frac{9}{4} = \frac{18}{12} = \frac{\cancel{18}^{3}}{\cancel{12}_{2}} = \frac{3}{2}$
[Multiplying and simplifying LHS]
RHS: $y \times x = \frac{9}{4} \times \frac{2}{3}$
$y \times x = \frac{\cancel{9}^{3}}{\cancel{4}_{2}} \times \frac{\cancel{2}^{1}}{\cancel{3}_{1}} = \frac{3 \times 1}{2 \times 1} = \frac{3}{2}$
$\frac{9}{4} \times \frac{2}{3} = \frac{18}{12} = \frac{\cancel{18}^{3}}{\cancel{12}_{2}} = \frac{3}{2}$
[Multiplying and simplifying RHS]
Since LHS = RHS ($\frac{3}{2} = \frac{3}{2}$), the property $x \times y = y \times x$ is verified for $x = \frac{2}{3}$ and $y = \frac{9}{4}$.
(c) Verify for $x = \frac{-5}{7}$, $y = \frac{14}{15}$
LHS: $x \times y = \frac{-5}{7} \times \frac{14}{15}$
$x \times y = \frac{\cancel{-5}^{-1}}{\cancel{7}_{1}} \times \frac{\cancel{14}^{2}}{\cancel{15}_{3}} = \frac{-1 \times 2}{1 \times 3} = \frac{-2}{3}$
$\frac{-5}{7} \times \frac{14}{15} = \frac{-70}{105} = \frac{\cancel{-70}^{-2}}{\cancel{105}_{3}} = \frac{-2}{3}$
[Multiplying and simplifying LHS]
RHS: $y \times x = \frac{14}{15} \times \frac{-5}{7}$
$y \times x = \frac{\cancel{14}^{2}}{\cancel{15}_{3}} \times \frac{\cancel{-5}^{-1}}{\cancel{7}_{1}} = \frac{2 \times -1}{3 \times 1} = \frac{-2}{3}$
$\frac{14}{15} \times \frac{-5}{7} = \frac{-70}{105} = \frac{\cancel{-70}^{-2}}{\cancel{105}_{3}} = \frac{-2}{3}$
[Multiplying and simplifying RHS]
Since LHS = RHS ($\frac{-2}{3} = \frac{-2}{3}$), the property $x \times y = y \times x$ is verified for $x = \frac{-5}{7}$ and $y = \frac{14}{15}$.
(d) Verify for $x = \frac{-3}{8}$, $y = \frac{-4}{9}$
LHS: $x \times y = \frac{-3}{8} \times \frac{-4}{9}$
$x \times y = \frac{\cancel{-3}^{-1}}{\cancel{8}_{2}} \times \frac{\cancel{-4}^{-1}}{\cancel{9}_{3}} = \frac{-1 \times -1}{2 \times 3} = \frac{1}{6}$
$\frac{-3}{8} \times \frac{-4}{9} = \frac{(-3) \times (-4)}{8 \times 9} = \frac{12}{72} = \frac{\cancel{12}^{1}}{\cancel{72}_{6}} = \frac{1}{6}$
[Multiplying and simplifying LHS]
RHS: $y \times x = \frac{-4}{9} \times \frac{-3}{8}$
$y \times x = \frac{\cancel{-4}^{-1}}{\cancel{9}_{3}} \times \frac{\cancel{-3}^{-1}}{\cancel{8}_{2}} = \frac{-1 \times -1}{3 \times 2} = \frac{1}{6}$
$\frac{-4}{9} \times \frac{-3}{8} = \frac{(-4) \times (-3)}{9 \times 8} = \frac{12}{72} = \frac{\cancel{12}^{1}}{\cancel{72}_{6}} = \frac{1}{6}$
[Multiplying and simplifying RHS]
Since LHS = RHS ($\frac{1}{6} = \frac{1}{6}$), the property $x \times y = y \times x$ is verified for $x = \frac{-3}{8}$ and $y = \frac{-4}{9}$.
Question 109. Verify the property x × (y × z) = (x × y) × z of rational numbers by using
(a) x = 1, y = $\frac{-1}{2}$ and z = $\frac{1}{4}$
(b) x = $\frac{2}{3}$ , y = $\frac{-3}{7}$ and z = $\frac{1}{2}$
(c) x = $\frac{-2}{7}$ , y = $\frac{-5}{6}$ and z = $\frac{1}{4}$
(d) x = 0, y = $\frac{1}{2}$
and What is the name of this property?
Answer:
We need to verify the property $x \times (y \times z) = (x \times y) \times z$ for the given values of $x, y, z$. This property is called the Associative Property of Multiplication.
(a) Verify for $x = 1$, $y = \frac{-1}{2}$, $z = \frac{1}{4}$
LHS: $x \times (y \times z) = 1 \times \left( \frac{-1}{2} \times \frac{1}{4} \right)$
$= 1 \times \left( \frac{-1 \times 1}{2 \times 4} \right)$
$= 1 \times \frac{-1}{8}$
$= \frac{-1}{8}$
RHS: $(x \times y) \times z = \left( 1 \times \frac{-1}{2} \right) \times \frac{1}{4}$
$= \left( \frac{1 \times (-1)}{1 \times 2} \right) \times \frac{1}{4}$
$= \frac{-1}{2} \times \frac{1}{4}$
$= \frac{-1 \times 1}{2 \times 4}$
$= \frac{-1}{8}$
Since LHS = RHS ($\frac{-1}{8} = \frac{-1}{8}$), the property is verified for this case.
(b) Verify for $x = \frac{2}{3}$, $y = \frac{-3}{7}$, $z = \frac{1}{2}$
LHS: $x \times (y \times z) = \frac{2}{3} \times \left( \frac{-3}{7} \times \frac{1}{2} \right)$
$= \frac{2}{3} \times \left( \frac{-3 \times 1}{7 \times 2} \right)$
$= \frac{2}{3} \times \frac{-3}{14}$
$= \frac{\cancel{2}^{1}}{\cancel{3}_{1}} \times \frac{\cancel{-3}^{-1}}{\cancel{14}_{7}}$
[Cancelling common factors]
$= \frac{1 \times (-1)}{1 \times 7}$
$= \frac{-1}{7}$
RHS: $(x \times y) \times z = \left( \frac{2}{3} \times \frac{-3}{7} \right) \times \frac{1}{2}$
$= \left( \frac{2 \times (-3)}{3 \times 7} \right) \times \frac{1}{2}$
$= \frac{-6}{21} \times \frac{1}{2}$
$= \frac{\cancel{-6}^{-1}}{\cancel{21}_{7}} \times \frac{1}{\cancel{2}_{1}}$
[Cancelling common factors]
$= \frac{-1 \times 1}{7 \times 1}$
$= \frac{-1}{7}$
Since LHS = RHS ($\frac{-1}{7} = \frac{-1}{7}$), the property is verified for this case.
(c) Verify for $x = \frac{-2}{7}$, $y = \frac{-5}{6}$, $z = \frac{1}{4}$
LHS: $x \times (y \times z) = \frac{-2}{7} \times \left( \frac{-5}{6} \times \frac{1}{4} \right)$
$= \frac{-2}{7} \times \left( \frac{-5 \times 1}{6 \times 4} \right)$
$= \frac{-2}{7} \times \frac{-5}{24}$
$= \frac{\cancel{-2}^{-1}}{7} \times \frac{-5}{\cancel{24}_{12}}$
[Cancelling common factors]
$= \frac{-1 \times (-5)}{7 \times 12}$
$= \frac{5}{84}$
RHS: $(x \times y) \times z = \left( \frac{-2}{7} \times \frac{-5}{6} \right) \times \frac{1}{4}$
$= \left( \frac{-2 \times (-5)}{7 \times 6} \right) \times \frac{1}{4}$
$= \frac{10}{42} \times \frac{1}{4}$
$= \frac{\cancel{10}^{5}}{\cancel{42}_{21}} \times \frac{1}{4}$
[Simplifying the first product]
$= \frac{5}{21} \times \frac{1}{4}$
$= \frac{5 \times 1}{21 \times 4}$
$= \frac{5}{84}$
Since LHS = RHS ($\frac{5}{84} = \frac{5}{84}$), the property is verified for this case.
(d) Verify for $x = 0$, $y = \frac{1}{2}$
The property $x \times (y \times z) = (x \times y) \times z$ involves three rational numbers $x$, $y$, and $z$. In this part, only the values for $x$ and $y$ are provided, while the value for $z$ is missing.
Therefore, the associative property of multiplication for three numbers cannot be verified with the given information for this case.
If we were simply asked to calculate $x \times y$, we would get:
$x \times y = 0 \times \frac{1}{2} = 0$
Name of the property:
The property $x \times (y \times z) = (x \times y) \times z$ is the Associative Property of Multiplication.
Question 110. Verify the property x × (y + z) = x × y + x × z of rational numbers by taking.
(a) x = $\frac{-1}{2}$ , y = $\frac{3}{4}$ , z = $\frac{1}{4}$
(b) x = $\frac{-1}{2}$ , y = $\frac{2}{3}$ , z = $\frac{3}{4}$
(c) x = $\frac{-2}{3}$ , y = $\frac{-4}{6}$ z = $\frac{-7}{9}$
(d) x = $\frac{-1}{5}$ , y = $\frac{2}{15}$ , z = $\frac{-3}{10}$
Answer:
Solution:
We need to verify the distributive property of multiplication over addition: $x \times (y + z) = x \times y + x \times z$.
(a) Verify for $x = \frac{-1}{2}$, $y = \frac{3}{4}$, $z = \frac{1}{4}$
LHS = $x \times (y + z) = \frac{-1}{2} \times \left( \frac{3}{4} + \frac{1}{4} \right) = \frac{-1}{2} \times \left( \frac{3+1}{4} \right) = \frac{-1}{2} \times \frac{4}{4} = \frac{-1}{2} \times 1 = \frac{-1}{2}$.
RHS = $x \times y + x \times z = \left( \frac{-1}{2} \times \frac{3}{4} \right) + \left( \frac{-1}{2} \times \frac{1}{4} \right) = \frac{-3}{8} + \frac{-1}{8} = \frac{-3-1}{8} = \frac{-4}{8} = \frac{\cancel{-4}^{-1}}{\cancel{8}_{2}} = \frac{-1}{2}$.
Since LHS = RHS, the property is verified for this case.
(b) Verify for $x = \frac{-1}{2}$, $y = \frac{2}{3}$, $z = \frac{3}{4}$
LHS = $x \times (y + z) = \frac{-1}{2} \times \left( \frac{2}{3} + \frac{3}{4} \right) = \frac{-1}{2} \times \left( \frac{2 \times 4}{12} + \frac{3 \times 3}{12} \right) = \frac{-1}{2} \times \left( \frac{8+9}{12} \right) = \frac{-1}{2} \times \frac{17}{12} = \frac{-17}{24}$.
RHS = $x \times y + x \times z = \left( \frac{-1}{2} \times \frac{2}{3} \right) + \left( \frac{-1}{2} \times \frac{3}{4} \right) = \left( \frac{\cancel{-1} \times \cancel{2}^{1}}{\cancel{2}_{1} \times 3} \right) + \frac{-3}{8} = \frac{-1}{3} + \frac{-3}{8} = \frac{-1 \times 8}{24} + \frac{-3 \times 3}{24} = \frac{-8}{24} + \frac{-9}{24} = \frac{-8-9}{24} = \frac{-17}{24}$.
Since LHS = RHS, the property is verified for this case.
(c) Verify for $x = \frac{-2}{3}$, $y = \frac{-4}{6}$, $z = \frac{-7}{9}$
Note $y = \frac{-4}{6} = \frac{-2}{3}$.
LHS = $x \times (y + z) = \frac{-2}{3} \times \left( \frac{-2}{3} + \frac{-7}{9} \right) = \frac{-2}{3} \times \left( \frac{-2 \times 3}{9} + \frac{-7}{9} \right) = \frac{-2}{3} \times \left( \frac{-6-7}{9} \right) = \frac{-2}{3} \times \frac{-13}{9} = \frac{(-2) \times (-13)}{3 \times 9} = \frac{26}{27}$.
RHS = $x \times y + x \times z = \left( \frac{-2}{3} \times \frac{-2}{3} \right) + \left( \frac{-2}{3} \times \frac{-7}{9} \right) = \frac{(-2) \times (-2)}{3 \times 3} + \frac{(-2) \times (-7)}{3 \times 9} = \frac{4}{9} + \frac{14}{27} = \frac{4 \times 3}{27} + \frac{14}{27} = \frac{12+14}{27} = \frac{26}{27}$.
Since LHS = RHS, the property is verified for this case.
(d) Verify for $x = \frac{-1}{5}$, $y = \frac{2}{15}$, $z = \frac{-3}{10}$
LHS = $x \times (y + z) = \frac{-1}{5} \times \left( \frac{2}{15} + \frac{-3}{10} \right)$. LCM(15, 10) = 30.
LHS $= \frac{-1}{5} \times \left( \frac{2 \times 2}{30} + \frac{-3 \times 3}{30} \right) = \frac{-1}{5} \times \left( \frac{4-9}{30} \right) = \frac{-1}{5} \times \frac{-5}{30} = \frac{-1}{5} \times \frac{\cancel{-5}^{-1}}{\cancel{30}_{6}} = \frac{-1}{5} \times \frac{-1}{6} = \frac{(-1) \times (-1)}{5 \times 6} = \frac{1}{30}$.
RHS = $x \times y + x \times z = \left( \frac{-1}{5} \times \frac{2}{15} \right) + \left( \frac{-1}{5} \times \frac{-3}{10} \right) = \frac{-2}{75} + \frac{3}{50}$. LCM(75, 50) = 150.
RHS $= \frac{-2 \times 2}{150} + \frac{3 \times 3}{150} = \frac{-4}{150} + \frac{9}{150} = \frac{-4+9}{150} = \frac{5}{150} = \frac{\cancel{5}^{1}}{\cancel{150}_{30}} = \frac{1}{30}$.
Since LHS = RHS, the property is verified for this case.
Question 111. Use the distributivity of multiplication of rational numbers over addition to simplify
(a) $\frac{3}{5}$ × $\left[ \frac{35}{24}+\frac{10}{1} \right]$
(b) $\frac{-5}{4}$ × $\left[ \frac{8}{5}+\frac{16}{15} \right]$
(c) $\frac{2}{7}$ × $\left[ \frac{7}{16}-\frac{21}{4} \right]$
(d) $\frac{3}{4}$ × $\left[ \frac{8}{9}-40 \right]$
Answer:
Solution:
We use the distributive property: $a \times (b + c) = a \times b + a \times c$ or $a \times (b - c) = a \times b - a \times c$.
(a) Simplify $\frac{3}{5}$ × $\left[ \frac{35}{24}+10 \right]$
$\frac{3}{5} \times \left( \frac{35}{24}+\frac{10}{1} \right) = \left( \frac{3}{5} \times \frac{35}{24} \right) + \left( \frac{3}{5} \times \frac{10}{1} \right)$
$= \left( \frac{\cancel{3}^{1}}{\cancel{5}_{1}} \times \frac{\cancel{35}^{7}}{\cancel{24}_{8}} \right) + \left( \frac{3}{\cancel{5}_{1}} \times \frac{\cancel{10}^{2}}{1} \right)$
$= \frac{7}{8} + 6 = \frac{7}{8} + \frac{48}{8} = \frac{7+48}{8} = \frac{55}{8}$
Answer (a): $\frac{55}{8}$
(b) Simplify $\frac{-5}{4}$ × $\left[ \frac{8}{5}+\frac{16}{15} \right]$
$\frac{-5}{4} \times \left( \frac{8}{5}+\frac{16}{15} \right) = \left( \frac{-5}{4} \times \frac{8}{5} \right) + \left( \frac{-5}{4} \times \frac{16}{15} \right)$
$= \left( \frac{\cancel{-5}^{-1}}{\cancel{4}_{1}} \times \frac{\cancel{8}^{2}}{\cancel{5}_{1}} \right) + \left( \frac{\cancel{-5}^{-1}}{\cancel{4}_{1}} \times \frac{\cancel{16}^{4}}{\cancel{15}_{3}} \right)$
$= -2 + \frac{-4}{3} = -2 - \frac{4}{3} = \frac{-6}{3} - \frac{4}{3} = \frac{-6-4}{3} = \frac{-10}{3}$
Answer (b): $\frac{-10}{3}$
(c) Simplify $\frac{2}{7}$ × $\left[ \frac{7}{16}-\frac{21}{4} \right]$
$\frac{2}{7} \times \left( \frac{7}{16}-\frac{21}{4} \right) = \left( \frac{2}{7} \times \frac{7}{16} \right) - \left( \frac{2}{7} \times \frac{21}{4} \right)$
$= \left( \frac{\cancel{2}^{1}}{\cancel{7}_{1}} \times \frac{\cancel{7}^{1}}{\cancel{16}_{8}} \right) - \left( \frac{\cancel{2}^{1}}{\cancel{7}_{1}} \times \frac{\cancel{21}^{3}}{\cancel{4}_{2}} \right)$
$= \frac{1}{8} - \frac{3}{2} = \frac{1}{8} - \frac{3 \times 4}{8} = \frac{1-12}{8} = \frac{-11}{8}$
Answer (c): $\frac{-11}{8}$
(d) Simplify $\frac{3}{4}$ × $\left[ \frac{8}{9}-40 \right]$
$\frac{3}{4} \times \left( \frac{8}{9}-\frac{40}{1} \right) = \left( \frac{3}{4} \times \frac{8}{9} \right) - \left( \frac{3}{4} \times \frac{40}{1} \right)$
$= \left( \frac{\cancel{3}^{1}}{\cancel{4}_{1}} \times \frac{\cancel{8}^{2}}{\cancel{9}_{3}} \right) - \left( \frac{3}{\cancel{4}_{1}} \times \frac{\cancel{40}^{10}}{1} \right)$
$= \frac{2}{3} - 30 = \frac{2}{3} - \frac{90}{3} = \frac{2-90}{3} = \frac{-88}{3}$
Answer (d): $\frac{-88}{3}$
Question 112. Simplify
(a) $\frac{32}{5}$ + $\frac{23}{11}$ × $\frac{22}{15}$
(b) $\frac{3}{7}$ × $\frac{28}{15}$ ÷ $\frac{14}{5}$
(c) $\frac{3}{7}$ + $\frac{-2}{21}$ × $\frac{-5}{6}$
(d) $\frac{7}{8}$ + $\frac{1}{16}$ - $\frac{-1}{12}$
Answer:
Solution (a):
Simplify $\frac{32}{5}$ + $\frac{23}{11}$ × $\frac{22}{15}$. Perform multiplication first.
$\frac{23}{11}$ × $\frac{22}{15} = \frac{23}{\cancel{11}_{1}} \times \frac{\cancel{22}^{2}}{15} = \frac{23 \times 2}{1 \times 15} = \frac{46}{15}$
Now, add the results:
$\frac{32}{5} + \frac{46}{15}$
The common denominator for 5 and 15 is 15.
$\frac{32 \times 3}{5 \times 3} + \frac{46}{15} = \frac{96}{15} + \frac{46}{15}$
$= \frac{96 + 46}{15} = \frac{142}{15}$
Answer (a): $\frac{142}{15}$
Solution (b):
Simplify $\frac{3}{7}$ × $\frac{28}{15}$ ÷ $\frac{14}{5}$. Perform multiplication and division from left to right. Division by a fraction is multiplication by its reciprocal.
$\frac{3}{7}$ × $\frac{28}{15}$ ÷ $\frac{14}{5} = \frac{3}{7}$ × $\frac{28}{15}$ × $\frac{5}{14}$
Multiply the fractions:
$= \frac{\cancel{3}^{1}}{\cancel{7}_{1}} \times \frac{\cancel{28}^{4}}{\cancel{15}_{5}} \times \frac{5}{14}$
$= \frac{1}{1} \times \frac{4}{5} \times \frac{5}{14}$
$= \frac{4}{\cancel{5}_{1}} \times \frac{\cancel{5}^{1}}{14} = \frac{4}{14}$
Simplify the resulting fraction:
$= \frac{\cancel{4}^{2}}{\cancel{14}_{7}} = \frac{2}{7}$
Answer (b): $\frac{2}{7}$
Solution (c):
Simplify $\frac{3}{7}$ + $\frac{-2}{21}$ × $\frac{-5}{6}$. Perform multiplication first.
$\frac{-2}{21}$ × $\frac{-5}{6} = \frac{\cancel{-2}^{-1}}{21} \times \frac{-5}{\cancel{6}_{3}} = \frac{-1 \times (-5)}{21 \times 3} = \frac{5}{63}$
Now, add the results:
$\frac{3}{7} + \frac{5}{63}$
The common denominator for 7 and 63 is 63.
$\frac{3 \times 9}{7 \times 9} + \frac{5}{63} = \frac{27}{63} + \frac{5}{63}$
$= \frac{27 + 5}{63} = \frac{32}{63}$
Answer (c): $\frac{32}{63}$
Solution (d):
Simplify $\frac{7}{8}$ + $\frac{1}{16}$ - $\frac{-1}{12}$. Perform addition and subtraction from left to right. Note that $-\frac{-1}{12} = +\frac{1}{12}$.
The expression is $\frac{7}{8} + \frac{1}{16} + \frac{1}{12}$.
Find the LCM of the denominators 8, 16, and 12.
Prime factorization of 8 is $2^3$.
Prime factorization of 16 is $2^4$.
Prime factorization of 12 is $2^2 \times 3$.
LCM(8, 16, 12) = $2^4 \times 3 = 16 \times 3 = 48$.
Convert each fraction to have a denominator of 48:
$\frac{7}{8} = \frac{7 \times 6}{8 \times 6} = \frac{42}{48}$
$\frac{1}{16} = \frac{1 \times 3}{16 \times 3} = \frac{3}{48}$
$\frac{1}{12} = \frac{1 \times 4}{12 \times 4} = \frac{4}{48}$
Now add the converted fractions:
$\frac{42}{48} + \frac{3}{48} + \frac{4}{48} = \frac{42 + 3 + 4}{48} = \frac{49}{48}$
Answer (d): $\frac{49}{48}$
Question 113. Identify the rational number that does not belong with the other three. Explain your reasoning
$\frac{-5}{11}$ , $\frac{-1}{2}$ , $\frac{-4}{9}$ , $\frac{-7}{3}$
Answer:
Solution:
We are given the following rational numbers:
$\frac{-5}{11}$, $\frac{-1}{2}$, $\frac{-4}{9}$, $\frac{-7}{3}$
Let's consider the values of these numbers:
$\frac{-5}{11} \approx -0.4545...$
$\frac{-1}{2} = -0.5$
$\frac{-4}{9} \approx -0.4444...$
$\frac{-7}{3} \approx -2.3333...$
Another way to look at this is by considering the absolute value of each number, which tells us the distance from zero on the number line.
$|\frac{-5}{11}| = \frac{5}{11}$
$|\frac{-1}{2}| = \frac{1}{2}$
$|\frac{-4}{9}| = \frac{4}{9}$
$|\frac{-7}{3}| = \frac{7}{3}$
We compare these values to 1:
$\frac{5}{11} < 1$ (since $5 < 11$)
$\frac{1}{2} < 1$ (since $1 < 2$)
$\frac{4}{9} < 1$ (since $4 < 9$)
$\frac{7}{3} > 1$ (since $7 > 3$)
The first three numbers ($\frac{-5}{11}$, $\frac{-1}{2}$, $\frac{-4}{9}$) have an absolute value less than 1 (they are proper fractions in terms of magnitude). They lie between -1 and 0 on the number line.
The last number ($\frac{-7}{3}$) has an absolute value greater than 1 (it is an improper fraction in terms of magnitude). It lies to the left of -1 on the number line.
Therefore, $\frac{-7}{3}$ is the rational number that does not belong with the other three based on its magnitude being greater than 1, while the others have magnitudes less than 1.
Answer:
The rational number that does not belong with the other three is $\frac{-7}{3}$.
Reasoning: The absolute values of $\frac{-5}{11}$, $\frac{-1}{2}$, and $\frac{-4}{9}$ are all less than 1. The absolute value of $\frac{-7}{3}$ is greater than 1.
Question 114. The cost of $\frac{19}{4}$ metres of wire is Rs. $\frac{171}{2}$ . Find the cost of one metre of the wire.
Answer:
Given:
Cost of $\frac{19}{4}$ metres of wire = $\textsf{₹} \frac{171}{2}$.
To Find:
The cost of one metre of wire.
Solution:
To find the cost of one metre of wire, we need to divide the total cost by the length of the wire.
Cost of 1 metre = $\frac{\text{Total Cost}}{\text{Length of wire}}$
Cost of 1 metre $= \textsf{₹} \frac{171}{2} \div \frac{19}{4}$
Dividing by a fraction is the same as multiplying by its reciprocal:
Cost of 1 metre $= \textsf{₹} \frac{171}{2} \times \frac{4}{19}$
Now, multiply the numerators and denominators, cancelling common factors where possible:
$= \textsf{₹} \frac{\cancel{171}^{9}}{\cancel{2}_{1}} \times \frac{\cancel{4}^{2}}{\cancel{19}_{1}}$
[Cancelling common factors, since $171 = 9 \times 19$ and $4 = 2 \times 2$]
$= \textsf{₹} \frac{9 \times 2}{1 \times 1}$
$= \textsf{₹} \frac{18}{1}$
$= \textsf{₹} 18$
Answer:
The cost of one metre of the wire is $\textsf{₹} 18$.
Question 115. A train travels $\frac{1445}{2}$ km in $\frac{17}{2}$ hours. Find the speed of the train in km/h.
Answer:
Given:
Distance traveled by the train = $\frac{1445}{2}$ km.
Time taken = $\frac{17}{2}$ hours.
To Find:
The speed of the train in km/h.
Solution:
The formula for speed is:
Speed = $\frac{\text{Distance}}{\text{Time}}$
Substitute the given values into the formula:
Speed $= \frac{\frac{1445}{2}}{\frac{17}{2}}$ km/h
Dividing by a fraction is the same as multiplying by the reciprocal of the divisor:
Speed $= \frac{1445}{2} \times \frac{2}{17}$
[Multiplying by the reciprocal of $\frac{17}{2}$]
Now, multiply the fractions, cancelling common factors:
Speed $= \frac{1445}{\cancel{2}_{1}} \times \frac{\cancel{2}^{1}}{17}$
[Cancelling 2 from numerator and denominator]
Speed $= \frac{1445}{1} \times \frac{1}{17} = \frac{1445}{17}$
To simplify $\frac{1445}{17}$, we divide 1445 by 17.
$1445 \div 17 = 85$ (Since $17 \times 80 = 1360$ and $17 \times 5 = 85$, so $1360 + 85 = 1445$).
Speed $= \frac{\cancel{1445}^{85}}{\cancel{17}_{1}} = 85$
[Simplifying the fraction]
The speed of the train is 85 km/h.
Answer:
The speed of the train is 85 km/h.
Question 116. If 16 shirts of equal size can be made out of 24 m of cloth, how much cloth is needed for making one shirt?
Answer:
Given:
Total length of cloth = 24 m.
Number of shirts made = 16.
To Find:
Length of cloth needed for one shirt.
Solution:
To find the amount of cloth needed for one shirt, we divide the total length of cloth by the number of shirts made.
Cloth needed for one shirt = $\frac{\text{Total length of cloth}}{\text{Number of shirts}}$
Cloth needed for one shirt $= \frac{24}{16}$ m
Simplify the fraction by dividing the numerator and the denominator by their greatest common divisor, which is 8.
$\frac{24}{16} = \frac{\cancel{24}^{3}}{\cancel{16}_{2}}$
[Simplifying the fraction]
Cloth needed for one shirt $= \frac{3}{2}$ m
The result can also be expressed as a mixed number or a decimal:
$\frac{3}{2} = 1 \frac{1}{2}$ m or $1.5$ m.
Answer:
The amount of cloth needed for making one shirt is $\frac{3}{2}$ m or 1.5 m.
Question 117. $\frac{7}{11}$ of all the money in Hamid’s bank account is Rs. 77,000. How much money does Hamid have in his bank account?
Answer:
Given:
$\frac{7}{11}$ of the total money in the bank account = $\textsf{₹} 77,000$.
To Find:
The total amount of money in Hamid's bank account.
Solution:
Let the total money in Hamid's bank account be $\textsf{₹} M$.
According to the question, $\frac{7}{11}$ of $M$ is $\textsf{₹} 77,000$. This can be written as an equation:
$\frac{7}{11} \times M = 77000$
... (i)
To find $M$, we need to isolate $M$. We can do this by multiplying both sides of the equation by the reciprocal of $\frac{7}{11}$, which is $\frac{11}{7}$.
$M = 77000 \div \frac{7}{11}$
$M = 77000 \times \frac{11}{7}$
Now, we can simplify the multiplication:
$M = \frac{77000}{1} \times \frac{11}{7}$
$M = \frac{\cancel{77000}^{11000}}{1} \times \frac{11}{\cancel{7}_{1}}$
[Cancelling 7 from numerator and denominator]
$M = 11000 \times 11$
$M = 121000$
So, the total money in Hamid's bank account is $\textsf{₹} 121,000$.
Answer:
Hamid has $\textsf{₹} 121,000$ in his bank account.
Question 118. A $117\frac{1}{3}$ m long rope is cut into equal pieces measuring $7\frac{1}{3}$ m each. How many such small pieces are these?
Answer:
Given:
Total length of the rope = $117\frac{1}{3}$ m.
Length of each small piece = $7\frac{1}{3}$ m.
To Find:
The number of small pieces the rope is cut into.
Solution:
First, convert the mixed numbers into improper fractions:
Total length = $117\frac{1}{3} = \frac{(117 \times 3) + 1}{3} = \frac{351 + 1}{3} = \frac{352}{3}$ m.
Length of each piece = $7\frac{1}{3} = \frac{(7 \times 3) + 1}{3} = \frac{21 + 1}{3} = \frac{22}{3}$ m.
To find the number of pieces, divide the total length of the rope by the length of each piece:
Number of pieces = $\frac{\text{Total length}}{\text{Length of each piece}}$
Number of pieces $= \frac{352}{3} \div \frac{22}{3}$
To divide by a fraction, multiply by its reciprocal:
Number of pieces $= \frac{352}{3} \times \frac{3}{22}$
[Multiplying by the reciprocal of $\frac{22}{3}$]
Now, perform the multiplication and cancel common factors:
Number of pieces $= \frac{352}{\cancel{3}_{1}} \times \frac{\cancel{3}^{1}}{22}$
[Cancelling 3 from numerator and denominator]
Number of pieces $= \frac{352}{22}$
Now, simplify the fraction $\frac{352}{22}$. Both numbers are divisible by 2:
$\frac{352}{22} = \frac{\cancel{352}^{176}}{\cancel{22}_{11}}$
[Dividing by 2]
Now, divide 176 by 11:
$\frac{176}{11} = 16$
[Performing division]
So, there are 16 small pieces.
Answer:
There are 16 such small pieces.
Question 119. $\frac{1}{6}$ of the class students are above average, $\frac{1}{4}$ are average and rest are below average. If there are 48 students in all, how many students are below average in the class?
Answer:
Given:
Total number of students in the class = 48.
Fraction of students above average = $\frac{1}{6}$.
Fraction of students average = $\frac{1}{4}$.
The remaining students are below average.
To Find:
The number of students who are below average.
Solution:
First, let's find the fraction of students who are either above average or average.
Fraction (above average + average) = Fraction above average + Fraction average
$= \frac{1}{6} + \frac{1}{4}$
To add these fractions, find the least common multiple (LCM) of the denominators 6 and 4. The LCM(6, 4) is 12.
$= \frac{1 \times 2}{6 \times 2} + \frac{1 \times 3}{4 \times 3} = \frac{2}{12} + \frac{3}{12}$
$= \frac{2+3}{12} = \frac{5}{12}$
So, $\frac{5}{12}$ of the students are either above average or average.
The fraction of students who are below average is the total fraction of students (which is 1) minus the fraction of students who are above average or average.
Fraction below average = $1 - \text{Fraction (above average + average)}$
$= 1 - \frac{5}{12}$
$= \frac{12}{12} - \frac{5}{12} = \frac{12-5}{12} = \frac{7}{12}$
Thus, $\frac{7}{12}$ of the students are below average.
To find the number of students below average, multiply the fraction of below average students by the total number of students.
Number of students below average = Fraction below average $\times$ Total number of students
$= \frac{7}{12} \times 48$
$= \frac{7}{\cancel{12}_{1}} \times \cancel{48}^{4}$
$= 7 \times 4$
$= 28$
Therefore, there are 28 students who are below average in the class.
Answer:
There are 28 students below average in the class.
Question 120. $\frac{2}{5}$ of total number of students of a school come by car while $\frac{1}{4}$ of students come by bus to school. All the other students walk to school of which $\frac{1}{3}$ walk on their own and the rest are escorted by their parents. If 224 students come to school walking on their own, how many students study in that school?
Answer:
Given:
Fraction of students by car = $\frac{2}{5}$.
Fraction of students by bus = $\frac{1}{4}$.
Fraction of walking students walking on their own = $\frac{1}{3}$ of walking students.
Number of students walking on their own = 224.
To Find:
The total number of students in the school.
Solution:
Let the total number of students in the school be $T$.
The fraction of students who come by car or bus is:
Fraction (car + bus) = $\frac{2}{5} + \frac{1}{4} = \frac{8}{20} + \frac{5}{20} = \frac{13}{20}$
[Sum of fractions]
The fraction of students who walk to school is the remaining fraction:
Fraction (walking) = $1 - \frac{13}{20} = \frac{7}{20}$
[Remaining fraction]
Of the walking students, $\frac{1}{3}$ walk on their own. So, the fraction of total students who walk on their own is:
Fraction (walk on own) = $\frac{7}{20} \times \frac{1}{3} = \frac{7}{60}$
[Fraction of total]
We are given that 224 students walk on their own. This number corresponds to the fraction $\frac{7}{60}$ of the total students $T$.
$\frac{7}{60} \times T = 224$
... (i)
To find $T$, divide 224 by $\frac{7}{60}$ (or multiply by its reciprocal $\frac{60}{7}$):
$T = 224 \times \frac{60}{7}$
[Solving for T]
Simplify:
$T = \cancel{224}^{32} \times \frac{60}{\cancel{7}_{1}} = 32 \times 60$
[Cancelling and multiplying]
$T = 1920$
So, there are 1920 students in the school.
Answer:
There are 1920 students in that school.
Question 121. Huma, Hubna and Seema received a total of Rs. 2,016 as monthly allowance from their mother such that Seema gets $\frac{1}{2}$ of what Huma gets and Hubna gets $1\frac{2}{3}$ times Seema’s share. How much money do the three sisters get individually?
Answer:
Given:
Total monthly allowance received by Huma, Hubna, and Seema = $\textsf{₹}2016$.
Seema's share is half of Huma's share.
Hubna's share is $1\frac{2}{3}$ times Seema's share.
Solution:
Let the share of Huma be $H$, the share of Hubna be $U$, and the share of Seema be $S$.
According to the problem, the total allowance is $\textsf{₹}2016$.
So, we have the equation:
$H + U + S = 2016$
We are given the following relationships between their shares:
$S = \frac{1}{2} H$
From this, we can express H in terms of S:
$H = 2S$
We are also given that Hubna's share is $1\frac{2}{3}$ times Seema's share.
$1\frac{2}{3} = \frac{1 \times 3 + 2}{3} = \frac{5}{3}$
So, we have:
$U = \frac{5}{3} S$
Now, substitute the expressions for $H$ and $U$ in terms of $S$ into the total allowance equation:
$(2S) + (\frac{5}{3} S) + S = 2016$
To solve for $S$, combine the terms on the left side:
$2S + \frac{5}{3} S + 1S = 2016$
Find a common denominator (which is 3) to add the coefficients of $S$:
$(\frac{6}{3})S + (\frac{5}{3})S + (\frac{3}{3})S = 2016$
$(\frac{6+5+3}{3})S = 2016$
$\frac{14}{3} S = 2016$
Now, isolate $S$ by multiplying both sides by $\frac{3}{14}$:
$S = 2016 \times \frac{3}{14}$
$S = \frac{2016}{14} \times 3$
Divide 2016 by 14:
$\frac{2016}{14} = 144$
$S = 144 \times 3$
$S = 432$
So, Seema's share is $\textsf{₹}432$.
Now, calculate Huma's share using $H = 2S$:
$H = 2 \times 432$
$H = 864$
So, Huma's share is $\textsf{₹}864$.
Finally, calculate Hubna's share using $U = \frac{5}{3} S$:
$U = \frac{5}{3} \times 432$
$U = 5 \times \frac{432}{3}$
$U = 5 \times 144$
$U = 720$
So, Hubna's share is $\textsf{₹}720$.
Let's verify the total: $864 + 720 + 432 = 1584 + 432 = 2016$. This matches the given total.
Answer:
The money received individually by the three sisters is:
Huma's share = $\textsf{₹}864$
Hubna's share = $\textsf{₹}720$
Seema's share = $\textsf{₹}432$
Question 122. A mother and her two daughters got a room constructed for Rs. 62,000. The elder daughter contributes $\frac{3}{8}$ of her mother’s contribution while the younger daughter contributes $\frac{1}{2}$ of her mother’s share. How much do the three contribute individually?
Answer:
Given:
Total cost of room construction = $\textsf{₹}62000$.
Elder daughter's contribution is $\frac{3}{8}$ of mother's contribution.
Younger daughter's contribution is $\frac{1}{2}$ of mother's share.
Solution:
Let the contribution of the mother be $M$, the contribution of the elder daughter be $E$, and the contribution of the younger daughter be $Y$.
The total cost is the sum of their contributions:
$M + E + Y = 62000$
According to the problem, the elder daughter's contribution is $\frac{3}{8}$ of the mother's contribution:
$E = \frac{3}{8} M$
The younger daughter's contribution is $\frac{1}{2}$ of the mother's share:
$Y = \frac{1}{2} M$
Now, substitute the expressions for $E$ and $Y$ in terms of $M$ into the total cost equation:
$M + \frac{3}{8} M + \frac{1}{2} M = 62000$
To solve for $M$, combine the terms on the left side by finding a common denominator, which is 8:
$\frac{8}{8} M + \frac{3}{8} M + \frac{4}{8} M = 62000$
$(\frac{8+3+4}{8}) M = 62000$
$\frac{15}{8} M = 62000$
Multiply both sides by $\frac{8}{15}$ to find $M$:
$M = 62000 \times \frac{8}{15}$
$M = \frac{62000 \times 8}{15}$
Simplify the fraction:
$M = \frac{496000}{15}$
Divide the numerator and denominator by 5:
$M = \frac{\cancel{496000}^{99200}}{\cancel{15}_{3}}$
$M = \frac{99200}{3}$
So, the mother's contribution is $\textsf{₹}\frac{99200}{3}$.
Now, calculate the elder daughter's contribution using $E = \frac{3}{8} M$:
$E = \frac{3}{8} \times \frac{99200}{3}$
$E = \frac{\cancel{3}}{8} \times \frac{99200}{\cancel{3}}$
$E = \frac{99200}{8}$
$E = 12400$
So, the elder daughter's contribution is $\textsf{₹}12400$.
Finally, calculate the younger daughter's contribution using $Y = \frac{1}{2} M$:
$Y = \frac{1}{2} \times \frac{99200}{3}$
$Y = \frac{99200}{6}$
Divide the numerator and denominator by 2:
$Y = \frac{\cancel{99200}^{49600}}{\cancel{6}_{3}}$
$Y = \frac{49600}{3}$
So, the younger daughter's contribution is $\textsf{₹}\frac{49600}{3}$.
Let's verify the total contribution:
$M + E + Y = \frac{99200}{3} + 12400 + \frac{49600}{3}$
$ = \frac{99200 + 49600}{3} + 12400$
$ = \frac{148800}{3} + 12400$
$ = 49600 + 12400$
$ = 62000$
The total matches the given cost.
Answer:
The contributions of the mother and her two daughters are:
Mother's contribution = $\textsf{₹}\frac{99200}{3}$
Elder daughter's contribution = $\textsf{₹}12400$
Younger daughter's contribution = $\textsf{₹}\frac{49600}{3}$
Question 123. Tell which property allows you to compare
$\frac{2}{3}$ × $\left[ \frac{3}{4}×\frac{5}{7} \right]$ and $\left[ \frac{2}{3}×\frac{5}{7} \right]$ × $\frac{3}{4}$
Answer:
We are asked to compare the two expressions:
Expression 1: $\frac{2}{3} \times \left( \frac{3}{4} \times \frac{5}{7} \right)$
Expression 2: $\left( \frac{2}{3} \times \frac{5}{7} \right) \times \frac{3}{4}$
Solution:
Let the three rational numbers be $a = \frac{2}{3}$, $b = \frac{3}{4}$, and $c = \frac{5}{7}$.
Expression 1 can be written as $a \times (b \times c)$.
Expression 2 can be written as $(a \times c) \times b$.
We can show that these two expressions are equal by applying the properties of multiplication for rational numbers.
Start with Expression 1:
$a \times (b \times c)$
Using the Commutative Property of Multiplication, we can change the order of the factors inside the parenthesis $(b \times c)$ to $(c \times b)$.
$a \times (b \times c) = a \times (c \times b)$
$= a \times (c \times b)$
(Commutative Property)
Now, using the Associative Property of Multiplication, which states that the grouping of factors in a multiplication does not change the product, we can regroup the terms.
$a \times (c \times b) = (a \times c) \times b$
$= (a \times c) \times b$
(Associative Property)
This matches Expression 2.
Thus, $\frac{2}{3} \times \left( \frac{3}{4} \times \frac{5}{7} \right) = \left( \frac{2}{3} \times \frac{5}{7} \right) \times \frac{3}{4}$.
The fact that these two expressions are equal allows us to compare them and state their equality.
The properties that allow us to establish this equality and thus compare the two expressions are the Commutative Property of Multiplication and the Associative Property of Multiplication for rational numbers.
Answer:
The properties that allow you to compare these two expressions (by showing they are equal) are the Associative Property of Multiplication and the Commutative Property of Multiplication for rational numbers.
Question 124. Name the property used in each of the following.
(i) $-\frac{7}{11}$ × $\frac{-3}{5}$ = $\frac{-3}{5}$ × $\frac{-7}{11}$
(ii) $-\frac{2}{3}$ × $\left[ \frac{3}{4}+\frac{-1}{2} \right]$ = $\left[ \frac{-2}{3}×\frac{3}{4} \right]$ + $\left[ \frac{-2}{3}×\frac{-1}{2} \right]$
(iii) $\frac{1}{3}$ + $\left[ \frac{4}{9}+\left( \frac{-4}{3} \right) \right]$ = $\left[ \frac{1}{3}+\frac{4}{9} \right]$ + $\left[ \frac{-4}{3} \right]$
(iv) $\frac{-2}{7}$ + 0 = 0 + $\frac{-2}{7}$ = $\frac{-2}{7}$
(v) $\frac{3}{8}$ × 1 = 1 × $\frac{3}{8}$ = $\frac{3}{8}$
Answer:
We need to identify the property used in each given equation involving rational numbers.
(i) $-\frac{7}{11}$ × $\frac{-3}{5}$ = $\frac{-3}{5}$ × $\frac{-7}{11}$
This equation shows that the order of multiplication of two rational numbers does not affect the product. This is the definition of the Commutative Property of Multiplication.
Property used: Commutative Property of Multiplication.
(ii) $-\frac{2}{3}$ × $\left[ \frac{3}{4}+\frac{-1}{2} \right]$ = $\left[ \frac{-2}{3}×\frac{3}{4} \right]$ + $\left[ \frac{-2}{3}×\frac{-1}{2} \right]$
This equation shows that multiplying a rational number by the sum of two other rational numbers gives the same result as multiplying the rational number by each of the two numbers separately and then adding the products. This is the definition of the Distributive Property of Multiplication over Addition.
Property used: Distributive Property of Multiplication over Addition.
(iii) $\frac{1}{3}$ + $\left[ \frac{4}{9}+\left( \frac{-4}{3} \right) \right]$ = $\left[ \frac{1}{3}+\frac{4}{9} \right]$ + $\left[ \frac{-4}{3} \right]$
This equation shows that the grouping of three rational numbers in an addition does not affect the sum. This is the definition of the Associative Property of Addition.
Property used: Associative Property of Addition.
(iv) $\frac{-2}{7}$ + 0 = 0 + $\frac{-2}{7}$ = $\frac{-2}{7}$
This equation shows that adding 0 to any rational number results in the same rational number. This property is related to the additive identity element, which is 0 for rational numbers.
Property used: Additive Identity Property.
(v) $\frac{3}{8}$ × 1 = 1 × $\frac{3}{8}$ = $\frac{3}{8}$
This equation shows that multiplying any rational number by 1 results in the same rational number. This property is related to the multiplicative identity element, which is 1 for rational numbers.
Property used: Multiplicative Identity Property.
Question 125. Find the multiplicative inverse of
(i) $-1\frac{1}{8}$
(ii) $3\frac{1}{3}$
Answer:
Solution:
The multiplicative inverse of a non-zero rational number $a$ is the rational number $b$ such that $a \times b = 1$. If the rational number is in the form $\frac{p}{q}$ (where $p \neq 0, q \neq 0$), its multiplicative inverse is $\frac{q}{p}$.
(i) Find the multiplicative inverse of $-1\frac{1}{8}$.
First, convert the mixed number $-1\frac{1}{8}$ into an improper fraction:
$-1\frac{1}{8} = -(1 \times 8 + 1)/8 = -\frac{9}{8}$
Now, find the reciprocal of $-\frac{9}{8}$. The reciprocal is obtained by swapping the numerator and the denominator.
Multiplicative inverse of $-\frac{9}{8}$ is $\frac{8}{-9}$ or $-\frac{8}{9}$.
Verification: $(-\frac{9}{8}) \times (-\frac{8}{9}) = \frac{(-9) \times (-8)}{8 \times 9} = \frac{72}{72} = 1$.
(ii) Find the multiplicative inverse of $3\frac{1}{3}$.
First, convert the mixed number $3\frac{1}{3}$ into an improper fraction:
$3\frac{1}{3} = (3 \times 3 + 1)/3 = \frac{10}{3}$
Now, find the reciprocal of $\frac{10}{3}$.
Multiplicative inverse of $\frac{10}{3}$ is $\frac{3}{10}$.
Verification: $(\frac{10}{3}) \times (\frac{3}{10}) = \frac{10 \times 3}{3 \times 10} = \frac{30}{30} = 1$.
Answer:
(i) The multiplicative inverse of $-1\frac{1}{8}$ is $-\frac{8}{9}$.
(ii) The multiplicative inverse of $3\frac{1}{3}$ is $\frac{3}{10}$.
Question 126. Arrange the numbers $\frac{1}{4}$ , $\frac{13}{16}$ , $\frac{5}{8}$ in the descending order
Answer:
Solution:
To arrange the given rational numbers in descending order, we need to compare them. The easiest way to compare fractions is to express them with a common denominator.
The given numbers are $\frac{1}{4}$, $\frac{13}{16}$, and $\frac{5}{8}$.
The denominators are 4, 16, and 8.
Let's find the Least Common Multiple (LCM) of the denominators 4, 16, and 8.
$\begin{array}{c|cc} 2 & 4 \;, & 16 \;, & 8 \\ \hline 2 & 2 \; , & 8 \; , & 4 \\ \hline 2 & 1 \; , & 4 \; , & 2 \\ \hline 2 & 1 \; , & 2 \; , & 1 \\ \hline & 1 \; , & 1 \; , & 1 \end{array}$
LCM(4, 16, 8) = $2 \times 2 \times 2 \times 2 = 16$.
Now, we convert each fraction to an equivalent fraction with a denominator of 16:
For $\frac{1}{4}$: Multiply numerator and denominator by $\frac{16}{4} = 4$.
$\frac{1}{4} = \frac{1 \times 4}{4 \times 4} = \frac{4}{16}$
For $\frac{13}{16}$: The denominator is already 16.
$\frac{13}{16}$
For $\frac{5}{8}$: Multiply numerator and denominator by $\frac{16}{8} = 2$.
$\frac{5}{8} = \frac{5 \times 2}{8 \times 2} = \frac{10}{16}$
Now we have the fractions with the same denominator: $\frac{4}{16}$, $\frac{13}{16}$, and $\frac{10}{16}$.
To arrange them in descending order (from largest to smallest), we compare their numerators: 4, 13, and 10.
Arranging the numerators in descending order: 13, 10, 4.
This corresponds to the fractions: $\frac{13}{16}$, $\frac{10}{16}$, $\frac{4}{16}$.
Replacing these with the original fractions:
$\frac{13}{16}$ corresponds to $\frac{13}{16}$.
$\frac{10}{16}$ corresponds to $\frac{5}{8}$.
$\frac{4}{16}$ corresponds to $\frac{1}{4}$.
So, the numbers in descending order are $\frac{13}{16}$, $\frac{5}{8}$, $\frac{1}{4}$.
Answer:
The numbers arranged in descending order are:
$\frac{13}{16}$, $\frac{5}{8}$, $\frac{1}{4}$
Question 127. The product of two rational numbers is $\frac{-14}{27}$. If one of the numbers be $\frac{7}{9}$ , find the other.
Answer:
Given:
Product of two rational numbers = $-\frac{14}{27}$.
One of the numbers = $\frac{7}{9}$.
To Find:
The other rational number.
Solution:
Let the other rational number be $x$.
According to the problem, the product of the two rational numbers is $-\frac{14}{27}$.
We can write this as an equation:
$\text{(One number)} \times \text{(Other number)} = \text{Product}$
$\frac{7}{9} \times x = -\frac{14}{27}$
To find the value of $x$, we need to isolate $x$ on one side of the equation. We can do this by dividing both sides by $\frac{7}{9}$.
$x = -\frac{14}{27} \div \frac{7}{9}$
Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of $\frac{7}{9}$ is $\frac{9}{7}$.
$x = -\frac{14}{27} \times \frac{9}{7}$
Now, we multiply the two fractions. We can simplify by cancelling common factors between the numerators and denominators before multiplying.
We can cancel 14 in the numerator with 7 in the denominator (both are divisible by 7): $14 \div 7 = 2$ and $7 \div 7 = 1$.
We can cancel 9 in the numerator with 27 in the denominator (both are divisible by 9): $9 \div 9 = 1$ and $27 \div 9 = 3$.
So, the expression becomes:
$x = \frac{-\cancel{14}^2}{\cancel{27}^3} \times \frac{\cancel{9}^1}{\cancel{7}^1}$
Now, multiply the simplified fractions:
$x = \frac{-2}{3} \times \frac{1}{1}$
$x = \frac{-2 \times 1}{3 \times 1}$
$x = -\frac{2}{3}$
Answer:
The other rational number is $-\frac{2}{3}$.
Question 128. By what numbers should we multiply $\frac{-15}{20}$ so that the product may be $\frac{-5}{7}$ ?
Answer:
Given:
The number to be multiplied is $-\frac{15}{20}$.
The desired product is $-\frac{5}{7}$.
To Find:
The number we should multiply by.
Solution:
Let the required number be $x$.
According to the problem, if we multiply $-\frac{15}{20}$ by $x$, the product is $-\frac{5}{7}$.
We can write this as an equation:
$-\frac{15}{20} \times x = -\frac{5}{7}$
To find the value of $x$, we need to isolate $x$. We can do this by dividing both sides of the equation by $-\frac{15}{20}$.
$x = -\frac{5}{7} \div (-\frac{15}{20})$
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of $-\frac{15}{20}$ is $-\frac{20}{15}$.
$x = -\frac{5}{7} \times (-\frac{20}{15})$
When multiplying two negative numbers, the result is positive. So, the product will be positive.
$x = \frac{5}{7} \times \frac{20}{15}$
Now, we can simplify the multiplication by cancelling common factors between the numerators and denominators.
We can cancel 5 in the numerator with 15 in the denominator (both are divisible by 5): $5 \div 5 = 1$ and $15 \div 5 = 3$.
So, the expression becomes:
$x = \frac{\cancel{5}^1}{7} \times \frac{20}{\cancel{15}^3}$
Now, multiply the simplified fractions:
$x = \frac{1}{7} \times \frac{20}{3}$
$x = \frac{1 \times 20}{7 \times 3}$
$x = \frac{20}{21}$
Answer:
We should multiply $-\frac{15}{20}$ by $\frac{20}{21}$ to get the product $-\frac{5}{7}$.
Question 129. By what number should we multiply $\frac{-8}{13}$ so that the product may be 24?
Answer:
Given:
The number to be multiplied is $-\frac{8}{13}$.
The desired product is 24.
To Find:
The number we should multiply by.
Solution:
Let the required number be $x$.
According to the problem, if we multiply $-\frac{8}{13}$ by $x$, the product is 24.
We can write this as an equation:
$-\frac{8}{13} \times x = 24$
To find the value of $x$, we need to isolate $x$. We can do this by dividing both sides of the equation by $-\frac{8}{13}$.
$x = 24 \div (-\frac{8}{13})$
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of $-\frac{8}{13}$ is $-\frac{13}{8}$.
$x = 24 \times (-\frac{13}{8})$
We can write 24 as a fraction $\frac{24}{1}$:
$x = \frac{24}{1} \times (-\frac{13}{8})$
Now, we can simplify the multiplication by cancelling common factors between the numerator (24) and the denominator (8). Both are divisible by 8.
$x = \frac{\cancel{24}^3}{1} \times (-\frac{13}{\cancel{8}^1})$
Multiply the simplified terms:
$x = 3 \times (-13)$
$x = -39$
Answer:
We should multiply $-\frac{8}{13}$ by $-39$ so that the product may be 24.
Question 130. The product of two rational numbers is –7. If one of the number is –5, find the other?
Answer:
Given:
Product of two rational numbers = $-7$.
One of the numbers = $-5$.
To Find:
The other rational number.
Solution:
Let the other rational number be $x$.
According to the problem, the product of the two rational numbers is $-7$.
We can write this as an equation:
$\text{(One number)} \times \text{(Other number)} = \text{Product}$
$-5 \times x = -7$
To find the value of $x$, we need to isolate $x$ on one side of the equation. We can do this by dividing both sides by $-5$.
$x = \frac{-7}{-5}$
When dividing a negative number by a negative number, the result is positive.
$x = \frac{7}{5}$
The other rational number is $\frac{7}{5}$. This can also be expressed as a mixed number $1\frac{2}{5}$ or a decimal $1.4$. However, the question involves integers and implies a rational number, so $\frac{7}{5}$ is the most appropriate form.
Answer:
The other rational number is $\frac{7}{5}$.
Question 131. Can you find a rational number whose multiplicative inverse is –1?
Answer:
To Determine:
Whether there exists a rational number whose multiplicative inverse is $-1$, and if so, find that number.
Solution:
Let the rational number be $x$.
The multiplicative inverse of a rational number $x$ is a number $y$ such that $x \times y = 1$.
In this problem, we are given that the multiplicative inverse of the rational number $x$ is $-1$.
According to the definition of multiplicative inverse, we can write the equation:
$x \times (-1) = 1$
To find the value of $x$, we need to solve this equation.
Divide both sides of the equation by $-1$:
$x = \frac{1}{-1}$
$x = -1$
The rational number is $-1$.
Let's verify this. The multiplicative inverse of $-1$ is $\frac{1}{-1}$, which is $-1$. So, the multiplicative inverse of $-1$ is indeed $-1$.
Since $-1$ can be expressed in the form $\frac{p}{q}$ (e.g., $\frac{-1}{1}$), it is a rational number.
Therefore, we can find a rational number whose multiplicative inverse is $-1$, and that number is $-1$ itself.
Answer:
Yes, the rational number whose multiplicative inverse is $-1$ is $\mathbf{-1}$.
Question 132. Find five rational numbers between 0 and 1.
Answer:
Given:
Two numbers, 0 and 1.
To Find:
Five rational numbers between 0 and 1.
Solution:
To find rational numbers between two given rational numbers, we can express both numbers as equivalent fractions with a common denominator. To find $n$ rational numbers, it is helpful to use a common denominator that is at least $n+1$ times a common denominator of the original numbers (if they are already fractions). Since we want to find 5 rational numbers, we can use a denominator of $5+1=6$ or any integer greater than 6.
Let's write 0 and 1 as fractions with a denominator of 6:
$0 = \frac{0}{1} = \frac{0 \times 6}{1 \times 6} = \frac{0}{6}$
$1 = \frac{1}{1} = \frac{1 \times 6}{1 \times 6} = \frac{6}{6}$
Now, we can find rational numbers between $\frac{0}{6}$ and $\frac{6}{6}$. These are fractions with a denominator of 6 and numerators between 0 and 6.
The integers between 0 and 6 are 1, 2, 3, 4, and 5.
So, the rational numbers between $\frac{0}{6}$ and $\frac{6}{6}$ are $\frac{1}{6}$, $\frac{2}{6}$, $\frac{3}{6}$, $\frac{4}{6}$, and $\frac{5}{6}$.
These are five rational numbers between 0 and 1.
Answer:
Five rational numbers between 0 and 1 are $\frac{1}{6}$, $\frac{2}{6}$, $\frac{3}{6}$, $\frac{4}{6}$, and $\frac{5}{6}$.
(Note: These can also be simplified as $\frac{1}{6}$, $\frac{1}{3}$, $\frac{1}{2}$, $\frac{2}{3}$, and $\frac{5}{6}$. Any five rational numbers between 0 and 1 are valid answers.)
Question 133. Find two rational numbers whose absolute value is $\frac{1}{5}$ .
Answer:
To Find:
Two rational numbers whose absolute value is $\frac{1}{5}$.
Solution:
The absolute value of a number is its distance from zero on the number line, regardless of direction. It is denoted by vertical bars around the number, e.g., $|x|$.
The absolute value of a positive number is the number itself: $|a| = a$ if $a \geq 0$.
The absolute value of a negative number is the opposite of the number: $|a| = -a$ if $a < 0$.
We are looking for rational numbers $x$ such that $|x| = \frac{1}{5}$.
This equation has two possibilities:
Case 1: The number is positive or zero.
If $x \geq 0$, then $|x| = x$. So, $x = \frac{1}{5}$.
Case 2: The number is negative.
If $x < 0$, then $|x| = -x$. So, $-x = \frac{1}{5}$.
To find $x$, multiply both sides by $-1$: $x = -\frac{1}{5}$.
Thus, the two rational numbers whose absolute value is $\frac{1}{5}$ are $\frac{1}{5}$ and $-\frac{1}{5}$.
Both $\frac{1}{5}$ and $-\frac{1}{5}$ are rational numbers because they can be expressed in the form $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.
Answer:
The two rational numbers whose absolute value is $\frac{1}{5}$ are $\frac{1}{5}$ and $-\frac{1}{5}$.
Question 134. From a rope 40 metres long, pieces of equal size are cut. If the length of one piece is $\frac{10}{3}$ metre, find the number of such pieces.
Answer:
Given:
Total length of the rope = 40 metres.
Length of each piece = $\frac{10}{3}$ metres.
To Find:
The number of pieces cut from the rope.
Solution:
To find the number of pieces, we need to divide the total length of the rope by the length of one piece.
Number of pieces = $\frac{\text{Total length of rope}}{\text{Length of one piece}}$
Number of pieces = $\frac{40}{\frac{10}{3}}$
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of $\frac{10}{3}$ is $\frac{3}{10}$.
Number of pieces = $40 \times \frac{3}{10}$
We can write 40 as a fraction $\frac{40}{1}$:
Number of pieces = $\frac{40}{1} \times \frac{3}{10}$
Now, we can simplify by cancelling the common factor 10 between the numerator (40) and the denominator (10).
Number of pieces = $\frac{\cancel{40}^4}{1} \times \frac{3}{\cancel{10}^1}$
Number of pieces = $\frac{4}{1} \times \frac{3}{1}$
Number of pieces = $4 \times 3$
Number of pieces = 12
So, 12 pieces of length $\frac{10}{3}$ metres each can be cut from a rope 40 metres long.
Answer:
The number of such pieces is 12.
Question 135. $5\frac{1}{2}$ metres long rope is cut into 12 equal pieces. What is the length of each piece?
Answer:
Given:
Total length of the rope = $5\frac{1}{2}$ metres.
Number of equal pieces = 12.
To Find:
The length of each piece.
Solution:
First, convert the total length of the rope from a mixed number to an improper fraction:
$5\frac{1}{2} = \frac{(5 \times 2) + 1}{2} = \frac{10 + 1}{2} = \frac{11}{2}$ metres.
To find the length of each equal piece, we need to divide the total length of the rope by the number of pieces.
Length of each piece = $\frac{\text{Total length of rope}}{\text{Number of pieces}}$
Length of each piece = $\frac{\frac{11}{2}}{12}$
Dividing by an integer is the same as multiplying by its reciprocal. The reciprocal of 12 is $\frac{1}{12}$.
Length of each piece = $\frac{11}{2} \times \frac{1}{12}$
Now, multiply the numerators and the denominators:
= $\frac{11 \times 1}{2 \times 12}$
= $\frac{11}{24}$
So, the length of each piece is $\frac{11}{24}$ metres.
Answer:
The length of each piece is $\mathbf{\frac{11}{24}}$ metres.
Question 136. Write the following rational numbers in the descending order.
$\frac{8}{7}$ , $\frac{-9}{8}$ , $\frac{-3}{2}$ , 0 , $\frac{2}{5}$
Answer:
Solution:
We are asked to arrange the following rational numbers in descending order (from largest to smallest):
$\frac{8}{7}$, $-\frac{9}{8}$, $-\frac{3}{2}$, 0, $\frac{2}{5}$
Let's first separate the positive, negative, and zero numbers. Positive numbers are always greater than zero and negative numbers. Zero is always greater than negative numbers.
Positive numbers: $\frac{8}{7}$, $\frac{2}{5}$
Zero: 0
Negative numbers: $-\frac{9}{8}$, $-\frac{3}{2}$
Step 1: Compare the positive numbers.
We need to compare $\frac{8}{7}$ and $\frac{2}{5}$. To compare them, we can find a common denominator or convert them to decimals.
Using a common denominator: The LCM of 7 and 5 is 35.
$\frac{8}{7} = \frac{8 \times 5}{7 \times 5} = \frac{40}{35}$
$\frac{2}{5} = \frac{2 \times 7}{5 \times 7} = \frac{14}{35}$
Comparing $\frac{40}{35}$ and $\frac{14}{35}$, since $40 > 14$, we have $\frac{40}{35} > \frac{14}{35}$.
So, $\frac{8}{7} > \frac{2}{5}$.
The positive numbers in descending order are $\frac{8}{7}$, $\frac{2}{5}$.
Step 2: Compare the negative numbers.
We need to compare $-\frac{9}{8}$ and $-\frac{3}{2}$. When comparing negative numbers, the number with the smaller absolute value is greater.
First, find the absolute values: $|-\frac{9}{8}| = \frac{9}{8}$ and $|-\frac{3}{2}| = \frac{3}{2}$.
Now, compare the absolute values $\frac{9}{8}$ and $\frac{3}{2}$. Find a common denominator. The LCM of 8 and 2 is 8.
$\frac{9}{8}$
$\frac{3}{2} = \frac{3 \times 4}{2 \times 4} = \frac{12}{8}$
Comparing $\frac{9}{8}$ and $\frac{12}{8}$, since $9 < 12$, we have $\frac{9}{8} < \frac{12}{8}$.
This means $|-\frac{9}{8}| < |-\frac{3}{2}|$.
For negative numbers, if $|a| < |b|$, then $a > b$.
So, $-\frac{9}{8} > -\frac{3}{2}$.
The negative numbers in descending order are $-\frac{9}{8}$, $-\frac{3}{2}$.
Step 3: Combine all the numbers in descending order.
The order from largest to smallest is: Positive numbers, then Zero, then Negative numbers.
So, the descending order is: (Positive numbers in descending order), 0, (Negative numbers in descending order).
Descending order: $\frac{8}{7}$, $\frac{2}{5}$, 0, $-\frac{9}{8}$, $-\frac{3}{2}$.
Answer:
The rational numbers in descending order are:
$\frac{8}{7}$, $\frac{2}{5}$, 0, $-\frac{9}{8}$, $-\frac{3}{2}$.
Question 137. Find
(i) 0 ÷ $\frac{2}{3}$
(ii) $\frac{1}{3}$ × $\frac{-5}{7}$ × $\frac{-21}{10}$
Answer:
Solution:
(i) Find 0 ÷ $\frac{2}{3}$
Dividing by a rational number is the same as multiplying by its multiplicative inverse (reciprocal).
The multiplicative inverse of $\frac{2}{3}$ is $\frac{3}{2}$.
So, $0 \div \frac{2}{3} = 0 \times \frac{3}{2}$.
Any number multiplied by zero is zero.
$0 \times \frac{3}{2} = 0$
Thus, $0 \div \frac{2}{3} = 0$.
(ii) Find $\frac{1}{3}$ × $\frac{-5}{7}$ × $\frac{-21}{10}$
We can multiply the numerators together and the denominators together.
$\frac{1}{3} \times \frac{-5}{7} \times \frac{-21}{10} = \frac{1 \times (-5) \times (-21)}{3 \times 7 \times 10}$
Before multiplying, we can cancel common factors from the numerator and the denominator.
Cancel 3 from the denominator with 21 from the numerator (since $21 = 3 \times 7$).
Cancel 7 from the denominator with 21 from the numerator.
Cancel 5 from the numerator with 10 from the denominator (since $10 = 5 \times 2$).
Let's perform the cancellations step-by-step:
$\frac{1}{\cancel{3}^1} \times \frac{-5}{7} \times \frac{-\cancel{21}^7}{10}$ (Cancelling 3 and 21 by dividing by 3)
$\frac{1}{1} \times \frac{-5}{\cancel{7}^1} \times \frac{-7}{\cancel{10}^2}$ (Cancelling 7 and 7 by dividing by 7, and 5 and 10 by dividing by 5)
Now, the expression is:
$\frac{1}{1} \times \frac{-1}{1} \times \frac{-1}{2}$
Multiply the simplified terms:
$\frac{1 \times (-1) \times (-1)}{1 \times 1 \times 2} = \frac{1}{2}$
Thus, $\frac{1}{3} \times \frac{-5}{7} \times \frac{-21}{10} = \frac{1}{2}$.
Answer:
(i) 0
(ii) $\frac{1}{2}$
Question 138. On a winter day the temperature at a place in Himachal Pradesh was –16°C. Convert it in degree Fahrenheit (°F) by using the formula.
$\frac{C}{5}=\frac{F\;-\;32}{9}$
Answer:
Given:
Temperature in Celsius ($C$) = $-16^\circ\text{C}$.
Formula for conversion between Celsius and Fahrenheit: $\frac{C}{5}=\frac{F\;-\;32}{9}$.
To Find:
The temperature in degree Fahrenheit ($F$).
Solution:
We are given the temperature in Celsius, $C = -16^\circ\text{C}$.
We need to use the formula $\frac{C}{5}=\frac{F\;-\;32}{9}$ to find the temperature in Fahrenheit, $F$.
Substitute $C = -16$ into the formula:
$\frac{-16}{5} = \frac{F - 32}{9}$
Now, we need to solve this equation for $F$.
Multiply both sides of the equation by 9:
$9 \times \left(\frac{-16}{5}\right) = 9 \times \left(\frac{F - 32}{9}\right)$
$\frac{9 \times (-16)}{5} = F - 32$
$\frac{-144}{5} = F - 32$
Convert the fraction $\frac{-144}{5}$ to a decimal:
$\frac{-144}{5} = -28.8$
So, the equation becomes:
$-28.8 = F - 32$
To isolate $F$, add 32 to both sides of the equation:
$F = -28.8 + 32$
$F = 3.2$
So, the temperature in Fahrenheit is $3.2^\circ\text{F}$.
Answer:
The temperature in degree Fahrenheit is $\mathbf{3.2^\circ\text{F}}$.
Question 139. Find the sum of additive inverse and multiplicative inverse of 7.
Answer:
Given:
The number is 7.
To Find:
The sum of the additive inverse and the multiplicative inverse of 7.
Solution:
First, let's find the additive inverse of 7.
The additive inverse of a number $a$ is the number $-a$ such that $a + (-a) = 0$.
For the number 7, the additive inverse is $-7$.
$7 + (-7) = 0$
Next, let's find the multiplicative inverse of 7.
The multiplicative inverse of a non-zero number $a$ is the number $\frac{1}{a}$ such that $a \times \frac{1}{a} = 1$.
For the number 7, the multiplicative inverse is $\frac{1}{7}$.
$7 \times \frac{1}{7} = 1$
Now, we need to find the sum of the additive inverse and the multiplicative inverse of 7.
Sum = (Additive inverse of 7) + (Multiplicative inverse of 7)
Sum = $-7 + \frac{1}{7}$
To add a whole number and a fraction, we write the whole number as a fraction with the same denominator as the other fraction. The denominator is 7.
$-7 = -\frac{7}{1} = -\frac{7 \times 7}{1 \times 7} = -\frac{49}{7}$
Now, perform the addition:
Sum = $-\frac{49}{7} + \frac{1}{7}$
Sum = $\frac{-49 + 1}{7}$
Sum = $\frac{-48}{7}$
Answer:
The sum of the additive inverse and multiplicative inverse of 7 is $\mathbf{-\frac{48}{7}}$.
Question 140. Find the product of additive inverse and multiplicative inverse of $-\frac{1}{3}$ .
Answer:
Given:
The number is $-\frac{1}{3}$.
To Find:
The product of the additive inverse and multiplicative inverse of $-\frac{1}{3}$.
Solution:
First, find the additive inverse of $-\frac{1}{3}$.
The additive inverse of a number $a$ is the number $-a$ such that $a + (-a) = 0$.
The additive inverse of $-\frac{1}{3}$ is $- (-\frac{1}{3}) = \frac{1}{3}$.
Next, find the multiplicative inverse of $-\frac{1}{3}$.
The multiplicative inverse of a non-zero number $a$ is the number $\frac{1}{a}$ such that $a \times \frac{1}{a} = 1$.
The multiplicative inverse of $-\frac{1}{3}$ is $\frac{1}{-\frac{1}{3}}$.
To find this, we take the reciprocal of $-\frac{1}{3}$, which is $-\frac{3}{1} = -3$.
So, the multiplicative inverse of $-\frac{1}{3}$ is $-3$.
Now, find the product of the additive inverse and the multiplicative inverse:
Product = (Additive inverse) $\times$ (Multiplicative inverse)
Product = $\frac{1}{3} \times (-3)$
Product = $\frac{1 \times (-3)}{3}$
Product = $\frac{-3}{3}$
Product = $-1$
Answer:
The product of the additive inverse and multiplicative inverse of $-\frac{1}{3}$ is $\mathbf{-1}$.
Question 141. The diagram shows the wingspans of different species of birds. Use the diagram to answer the question given below:

(a) How much longer is the wingspan of an Albatross than the wingspan of a Sea gull?
(b) How much longer is the wingspan of a Golden eagle than the wingspan of a Blue jay?
Answer:
Given:
Wingspans of different birds as provided in the diagram and text:
- Albatross: $5\frac{2}{3}$ m
- Golden eagle: $7\frac{1}{2}$ ft
- Great Horned Owl: $4\frac{1}{2}$ ft
- Sea gull: $2\frac{1}{2}$ ft
- Blue jay: $1\frac{1}{4}$ ft
The diagram shows these values plotted on a single numerical scale.
To Find:
(a) The difference in wingspan between an Albatross and a Sea gull.
(b) The difference in wingspan between a Golden eagle and a Blue jay.
Solution:
Based on the visual representation in the diagram using a single scale for all numerical values, we will calculate the differences directly using the given numbers.
(a) Difference in wingspan between Albatross and Sea gull:
Wingspan of Albatross = $5\frac{2}{3}$
Wingspan of Sea gull = $2\frac{1}{2}$
Convert the mixed numbers to improper fractions:
$5\frac{2}{3} = \frac{(5 \times 3) + 2}{3} = \frac{17}{3}$
$2\frac{1}{2} = \frac{(2 \times 2) + 1}{2} = \frac{5}{2}$
Subtract the Sea gull's wingspan from the Albatross's wingspan:
Difference = $5\frac{2}{3} - 2\frac{1}{2} = \frac{17}{3} - \frac{5}{2}$
Find a common denominator, which is LCM(3, 2) = 6.
$\frac{17}{3} = \frac{17 \times 2}{3 \times 2} = \frac{34}{6}$
$\frac{5}{2} = \frac{5 \times 3}{2 \times 3} = \frac{15}{6}$
Difference = $\frac{34}{6} - \frac{15}{6} = \frac{34 - 15}{6} = \frac{19}{6}$
Convert the improper fraction $\frac{19}{6}$ back to a mixed number:
$\frac{19}{6} = 3\frac{1}{6}$
(b) Difference in wingspan between Golden eagle and Blue jay:
Wingspan of Golden eagle = $7\frac{1}{2}$ ft
Wingspan of Blue jay = $1\frac{1}{4}$ ft
Convert the mixed numbers to improper fractions:
$7\frac{1}{2} = \frac{(7 \times 2) + 1}{2} = \frac{15}{2}$
$1\frac{1}{4} = \frac{(1 \times 4) + 1}{4} = \frac{5}{4}$
Subtract the Blue jay's wingspan from the Golden eagle's wingspan:
Difference = $7\frac{1}{2} - 1\frac{1}{4} = \frac{15}{2} - \frac{5}{4}$
Find a common denominator, which is LCM(2, 4) = 4.
$\frac{15}{2} = \frac{15 \times 2}{2 \times 2} = \frac{30}{4}$
$\frac{5}{4}$ (already has the denominator 4)
Difference = $\frac{30}{4} - \frac{5}{4} = \frac{30 - 5}{4} = \frac{25}{4}$
Convert the improper fraction $\frac{25}{4}$ back to a mixed number:
$\frac{25}{4} = 6\frac{1}{4}$
Since both the original values for Golden eagle and Blue jay are in feet, the difference is also in feet.
Answer:
(a) The wingspan of an Albatross is $\mathbf{3\frac{1}{6}}$ longer than the wingspan of a Sea gull (based on the numerical values presented in the diagram).
(b) The wingspan of a Golden eagle is $\mathbf{6\frac{1}{4}}$ ft longer than the wingspan of a Blue jay.
Question 142. Shalini has to cut out circles of diameter $1\frac{1}{4}$ cm from an aluminium strip of dimensions $8\frac{3}{4}$ cm by $1\frac{1}{4}$ cm. How many full circles can Shalini cut? Also calculate the wastage of the aluminium strip.
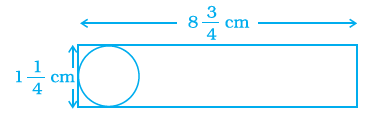
Answer:
Given:
Diameter of each circle = $1\frac{1}{4}$ cm.
Dimensions of the aluminium strip = $8\frac{3}{4}$ cm by $1\frac{1}{4}$ cm.
To Find:
The number of full circles that can be cut and the wastage of the aluminium strip.
Solution:
First, convert the given mixed numbers to improper fractions.
Diameter of circle = $1\frac{1}{4} = \frac{(1 \times 4) + 1}{4} = \frac{5}{4}$ cm.
Length of the aluminium strip = $8\frac{3}{4} = \frac{(8 \times 4) + 3}{4} = \frac{32 + 3}{4} = \frac{35}{4}$ cm.
Width of the aluminium strip = $1\frac{1}{4} = \frac{(1 \times 4) + 1}{4} = \frac{5}{4}$ cm.
The width of the strip ($\frac{5}{4}$ cm) is exactly equal to the diameter of the circle ($\frac{5}{4}$ cm). This means that only one row of circles can be cut across the width of the strip.
To find the number of circles that can be cut along the length of the strip, divide the length of the strip by the diameter of one circle:
Number of circles along the length = $\frac{\text{Length of strip}}{\text{Diameter of circle}}$
= $\frac{8\frac{3}{4}}{1\frac{1}{4}} = \frac{\frac{35}{4}}{\frac{5}{4}}$
= $\frac{35}{4} \div \frac{5}{4}$
= $\frac{35}{4} \times \frac{4}{5}$
= $\frac{35 \times \cancel{4}}{\cancel{4} \times 5} = \frac{35}{5} = 7$
Since the width allows for only one row, and 7 circles fit along the length, Shalini can cut out 7 full circles.
Now, calculate the wastage of the aluminium strip.
Wastage is the area of the strip minus the total area of the circles cut out.
Area of the aluminium strip = Length $\times$ Width
= $8\frac{3}{4} \text{ cm} \times 1\frac{1}{4} \text{ cm}$
= $\frac{35}{4} \times \frac{5}{4} \text{ cm}^2$
= $\frac{35 \times 5}{4 \times 4} \text{ cm}^2 = \frac{175}{16} \text{ cm}^2$
The diameter of one circle is $\frac{5}{4}$ cm, so the radius is $r = \frac{1}{2} \times \frac{5}{4} = \frac{5}{8}$ cm.
Area of one circle = $\pi r^2 = \pi \left( \frac{5}{8} \right)^2 = \pi \times \frac{5^2}{8^2} = \frac{25\pi}{64} \text{ cm}^2$.
Total area of 7 circles = $7 \times (\text{Area of one circle})$
= $7 \times \frac{25\pi}{64} \text{ cm}^2 = \frac{7 \times 25\pi}{64} \text{ cm}^2 = \frac{175\pi}{64} \text{ cm}^2$.
Wastage = Area of strip - Total area of 7 circles
= $\frac{175}{16} - \frac{175\pi}{64} \text{ cm}^2$
To express this with a common denominator:
= $\frac{175 \times 4}{16 \times 4} - \frac{175\pi}{64} \text{ cm}^2$
= $\frac{700}{64} - \frac{175\pi}{64} \text{ cm}^2$
= $\frac{700 - 175\pi}{64} \text{ cm}^2$
We can also factor out 175 from the numerator:
= $\frac{175(4 - \pi)}{64} \text{ cm}^2$
Answer:
Shalini can cut 7 full circles.
The wastage of the aluminium strip is $\mathbf{\left(\frac{175}{16} - \frac{175\pi}{64}\right)}$ $\mathbf{\text{cm}^2}$ or $\mathbf{\frac{175(4 - \pi)}{64}}$ $\mathbf{\text{cm}^2}$.
Question 143. One fruit salad recipe requires $\frac{1}{2}$ cup of sugar. Another recipe for thesame fruit salad requires 2 tablespoons of sugar. If 1 tablespoon isequivalent to $\frac{1}{16}$ cup, how much more sugar does the first reciperequire?
Answer:
Given:
Recipe 1 requires $\frac{1}{2}$ cup of sugar.
Recipe 2 requires 2 tablespoons of sugar.
Equivalence: 1 tablespoon = $\frac{1}{16}$ cup.
To Find:
How much more sugar the first recipe requires compared to the second recipe.
Solution:
To compare the amount of sugar in both recipes, we need to express them in the same unit. Let's convert the amount of sugar in Recipe 2 from tablespoons to cups using the given equivalence.
1 tablespoon = $\frac{1}{16}$ cup
Recipe 2 requires 2 tablespoons.
Amount of sugar in Recipe 2 (in cups) = 2 tablespoons $\times$ (conversion factor)
= $2 \times \left(\frac{1}{16} \text{ cup per tablespoon}\right)$
= $\frac{2}{1} \times \frac{1}{16}$ cups
= $\frac{2 \times 1}{1 \times 16}$ cups
= $\frac{2}{16}$ cups
Simplify the fraction:
= $\frac{\cancel{2}^1}{\cancel{16}^8}$ cups = $\frac{1}{8}$ cup.
So, Recipe 1 requires $\frac{1}{2}$ cup of sugar, and Recipe 2 requires $\frac{1}{8}$ cup of sugar.
To find how much more sugar the first recipe requires, we subtract the amount of sugar in Recipe 2 from the amount in Recipe 1.
Difference = Amount in Recipe 1 - Amount in Recipe 2
Difference = $\frac{1}{2} - \frac{1}{8}$
To subtract the fractions, find a common denominator. The LCM of 2 and 8 is 8.
Convert $\frac{1}{2}$ to a fraction with denominator 8:
$\frac{1}{2} = \frac{1 \times 4}{2 \times 4} = \frac{4}{8}$
Now, perform the subtraction:
Difference = $\frac{4}{8} - \frac{1}{8}$
Difference = $\frac{4 - 1}{8}$
Difference = $\frac{3}{8}$
So, the first recipe requires $\frac{3}{8}$ cup more sugar than the second recipe.
Answer:
The first recipe requires $\mathbf{\frac{3}{8}}$ cup more sugar than the second recipe.
Question 144. Four friends had a competition to see how far could they hop on one foot. The table given shows the distance covered by each.
| Name | Distance covered (km) |
|---|---|
| Seema | $\frac{1}{25}$ |
| Nancy | $\frac{1}{32}$ |
| Megha | $\frac{1}{40}$ |
| Soni | $\frac{1}{20}$ |
(a) How farther did Soni hop than Nancy?
(b) What is the total distance covered by Seema and Megha?
(c) Who walked farther, Nancy or Megha?
Answer:
Given:
Distances covered by four friends:
Seema: $\frac{1}{25}$ km
Nancy: $\frac{1}{32}$ km
Megha: $\frac{1}{40}$ km
Soni: $\frac{1}{20}$ km
To Find:
(a) The difference in distance between Soni and Nancy.
(b) The total distance covered by Seema and Megha.
(c) Who walked farther between Nancy and Megha.
Solution:
(a) How farther did Soni hop than Nancy?
To find how much farther Soni hopped than Nancy, we subtract Nancy's distance from Soni's distance.
Soni's distance = $\frac{1}{20}$ km
Nancy's distance = $\frac{1}{32}$ km
Difference = Soni's distance - Nancy's distance
= $\frac{1}{20} - \frac{1}{32}$
Find the LCM of the denominators 20 and 32.
Prime factorization of 20: $2^2 \times 5$
Prime factorization of 32: $2^5$
LCM(20, 32) = $2^5 \times 5 = 32 \times 5 = 160$.
Convert the fractions to have a denominator of 160:
$\frac{1}{20} = \frac{1 \times 8}{20 \times 8} = \frac{8}{160}$
$\frac{1}{32} = \frac{1 \times 5}{32 \times 5} = \frac{5}{160}$
Subtract the fractions:
Difference = $\frac{8}{160} - \frac{5}{160} = \frac{8 - 5}{160} = \frac{3}{160}$
(b) What is the total distance covered by Seema and Megha?
To find the total distance, we add Seema's distance and Megha's distance.
Seema's distance = $\frac{1}{25}$ km
Megha's distance = $\frac{1}{40}$ km
Total distance = Seema's distance + Megha's distance
= $\frac{1}{25} + \frac{1}{40}$
Find the LCM of the denominators 25 and 40.
Prime factorization of 25: $5^2$
Prime factorization of 40: $2^3 \times 5$
LCM(25, 40) = $2^3 \times 5^2 = 8 \times 25 = 200$.
Convert the fractions to have a denominator of 200:
$\frac{1}{25} = \frac{1 \times 8}{25 \times 8} = \frac{8}{200}$
$\frac{1}{40} = \frac{1 \times 5}{40 \times 5} = \frac{5}{200}$
Add the fractions:
Total distance = $\frac{8}{200} + \frac{5}{200} = \frac{8 + 5}{200} = \frac{13}{200}$
(c) Who walked farther, Nancy or Megha?
We need to compare Nancy's distance ($\frac{1}{32}$ km) and Megha's distance ($\frac{1}{40}$ km).
To compare fractions with the same numerator (in this case, 1), the fraction with the smaller denominator is greater.
Comparing the denominators 32 and 40, we have $32 < 40$.
Therefore, $\frac{1}{32} > \frac{1}{40}$.
Nancy's distance is $\frac{1}{32}$ km, and Megha's distance is $\frac{1}{40}$ km.
Since $\frac{1}{32} > \frac{1}{40}$, Nancy walked farther than Megha.
Answer:
(a) Soni hopped $\mathbf{\frac{3}{160}}$ km farther than Nancy.
(b) The total distance covered by Seema and Megha is $\mathbf{\frac{13}{200}}$ km.
(c) Nancy walked farther than Megha.
Question 145. The table given below shows the distances, in kilometres, between four villages of a state. To find the distance between two villages, locate the square where the row for one village and the column for the other village intersect.

(a) Compare the distance between Himgaon and Rawalpur to Sonapur and Ramgarh?
(b) If you drove from Himgaon to Sonapur and then from Sonapur to Rawalpur, how far would you drive?
Answer:
Given:
Distances between villages from the provided table:
Distance (Himgaon to Rawalpur) = $5\frac{1}{2}$ km
Distance (Sonapur to Ramgarh) = $6\frac{1}{4}$ km
Distance (Himgaon to Sonapur) = $4\frac{2}{3}$ km
Distance (Sonapur to Rawalpur) = $5\frac{5}{6}$ km
To Find:
(a) Comparison of the distance between Himgaon and Rawalpur with the distance between Sonapur and Ramgarh.
(b) The total distance driven from Himgaon to Sonapur and then to Rawalpur.
Solution:
(a) Compare the distance between Himgaon and Rawalpur to Sonapur and Ramgarh:
Distance (Himgaon to Rawalpur) = $5\frac{1}{2}$ km
Distance (Sonapur to Ramgarh) = $6\frac{1}{4}$ km
To compare these distances, convert the mixed numbers to improper fractions:
$5\frac{1}{2} = \frac{(5 \times 2) + 1}{2} = \frac{11}{2}$ km
$6\frac{1}{4} = \frac{(6 \times 4) + 1}{4} = \frac{25}{4}$ km
Now, compare $\frac{11}{2}$ and $\frac{25}{4}$. Find a common denominator, which is LCM(2, 4) = 4.
$\frac{11}{2} = \frac{11 \times 2}{2 \times 2} = \frac{22}{4}$
Comparing $\frac{22}{4}$ km and $\frac{25}{4}$ km:
Since the denominators are the same, compare the numerators: $22 < 25$.
Therefore, $\frac{22}{4} < \frac{25}{4}$.
This means $5\frac{1}{2}$ km $< 6\frac{1}{4}$ km.
The distance between Himgaon and Rawalpur is less than the distance between Sonapur and Ramgarh.
(b) If you drove from Himgaon to Sonapur and then from Sonapur to Rawalpur, how far would you drive?
The total distance is the sum of the distance from Himgaon to Sonapur and the distance from Sonapur to Rawalpur.
Distance (Himgaon to Sonapur) = $4\frac{2}{3}$ km
Distance (Sonapur to Rawalpur) = $5\frac{5}{6}$ km
Convert the mixed numbers to improper fractions:
$4\frac{2}{3} = \frac{(4 \times 3) + 2}{3} = \frac{12 + 2}{3} = \frac{14}{3}$ km
$5\frac{5}{6} = \frac{(5 \times 6) + 5}{6} = \frac{30 + 5}{6} = \frac{35}{6}$ km
Total distance = $\frac{14}{3} + \frac{35}{6}$
Find a common denominator for 3 and 6, which is LCM(3, 6) = 6.
Convert $\frac{14}{3}$ to a fraction with denominator 6:
$\frac{14}{3} = \frac{14 \times 2}{3 \times 2} = \frac{28}{6}$
Add the fractions:
Total distance = $\frac{28}{6} + \frac{35}{6} = \frac{28 + 35}{6} = \frac{63}{6}$
Simplify the fraction $\frac{63}{6}$ by dividing the numerator and denominator by their greatest common divisor, which is 3.
$\frac{63}{6} = \frac{63 \div 3}{6 \div 3} = \frac{21}{2}$
Convert the improper fraction back to a mixed number:
$\frac{21}{2} = 10\frac{1}{2}$
So, the total distance driven would be $10\frac{1}{2}$ km.
Answer:
(a) The distance between Himgaon and Rawalpur ($5\frac{1}{2}$ km) is less than the distance between Sonapur and Ramgarh ($6\frac{1}{4}$ km).
(b) If you drove from Himgaon to Sonapur and then from Sonapur to Rawalpur, you would drive a total of $\mathbf{10\frac{1}{2}}$ km.
Question 146. The table shows the portion of some common materials that are recycled.
| Material | Recycled |
|---|---|
| Paper | $\frac{5}{11}$ |
| Aluminium cans | $\frac{5}{8}$ |
| Glass | $\frac{2}{5}$ |
| Scrap | $\frac{3}{4}$ |
(a) Is the rational number expressing the amount of paper recycled more than $\frac{1}{2}$ or less than $\frac{1}{2}$ ?
(b) Which items have a recycled amount less than $\frac{1}{2}$ ?
(c) Is the quantity of aluminium cans recycled more (or less) thanhalf of the quantity of aluminium cans?
(d) Arrange the rate of recycling the materials from the greatest to the smallest.
Answer:
Given:
Recycled portions of materials:
Paper: $\frac{5}{11}$
Aluminium cans: $\frac{5}{8}$
Glass: $\frac{2}{5}$
Scrap: $\frac{3}{4}$
To Determine:
Answers to the given questions based on the recycled portions.
Solution:
(a) Is the rational number expressing the amount of paper recycled more than $\frac{1}{2}$ or less than $\frac{1}{2}$ ?
We need to compare $\frac{5}{11}$ and $\frac{1}{2}$.
To compare them, find a common denominator, which is LCM(11, 2) = 22.
$\frac{5}{11} = \frac{5 \times 2}{11 \times 2} = \frac{10}{22}$
$\frac{1}{2} = \frac{1 \times 11}{2 \times 11} = \frac{11}{22}$
Comparing $\frac{10}{22}$ and $\frac{11}{22}$, since $10 < 11$, we have $\frac{10}{22} < \frac{11}{22}$.
Thus, $\frac{5}{11} < \frac{1}{2}$.
(b) Which items have a recycled amount less than $\frac{1}{2}$ ?
We need to compare each recycled amount with $\frac{1}{2}$.
Paper: $\frac{5}{11}$. From part (a), we found $\frac{5}{11} < \frac{1}{2}$. So, Paper has a recycled amount less than $\frac{1}{2}$.
Aluminium cans: $\frac{5}{8}$. Compare $\frac{5}{8}$ and $\frac{1}{2}$. Common denominator is 8.
$\frac{1}{2} = \frac{1 \times 4}{2 \times 4} = \frac{4}{8}$.
Comparing $\frac{5}{8}$ and $\frac{4}{8}$, since $5 > 4$, we have $\frac{5}{8} > \frac{4}{8}$. So, Aluminium cans' recycled amount is not less than $\frac{1}{2}$.
Glass: $\frac{2}{5}$. Compare $\frac{2}{5}$ and $\frac{1}{2}$. Common denominator is 10.
$\frac{2}{5} = \frac{2 \times 2}{5 \times 2} = \frac{4}{10}$.
$\frac{1}{2} = \frac{1 \times 5}{2 \times 5} = \frac{5}{10}$.
Comparing $\frac{4}{10}$ and $\frac{5}{10}$, since $4 < 5$, we have $\frac{4}{10} < \frac{5}{10}$. So, Glass has a recycled amount less than $\frac{1}{2}$.
Scrap: $\frac{3}{4}$. Compare $\frac{3}{4}$ and $\frac{1}{2}$. Common denominator is 4.
$\frac{1}{2} = \frac{1 \times 2}{2 \times 2} = \frac{2}{4}$.
Comparing $\frac{3}{4}$ and $\frac{2}{4}$, since $3 > 2$, we have $\frac{3}{4} > \frac{2}{4}$. So, Scrap's recycled amount is not less than $\frac{1}{2}$.
The items with a recycled amount less than $\frac{1}{2}$ are Paper and Glass.
(c) Is the quantity of aluminium cans recycled more (or less) than half of the quantity of aluminium cans?
The quantity of aluminium cans recycled is given as $\frac{5}{8}$. Half of the quantity of aluminium cans would be represented by the fraction $\frac{1}{2}$.
We need to compare $\frac{5}{8}$ and $\frac{1}{2}$. From part (b), we found that $\frac{5}{8} > \frac{1}{2}$.
So, the quantity of aluminium cans recycled is more than half of the quantity of aluminium cans.
(d) Arrange the rate of recycling the materials from the greatest to the smallest.
We need to arrange the following fractions in descending order:
$\frac{5}{11}$, $\frac{5}{8}$, $\frac{2}{5}$, $\frac{3}{4}$
To compare these fractions, find a common denominator. The denominators are 11, 8, 5, and 4.
LCM(11, 8, 5, 4) = LCM($11, 2^3, 5, 2^2$) = $2^3 \times 5 \times 11 = 8 \times 5 \times 11 = 40 \times 11 = 440$.
Convert each fraction to have a denominator of 440:
Paper: $\frac{5}{11} = \frac{5 \times 40}{11 \times 40} = \frac{200}{440}$
Aluminium cans: $\frac{5}{8} = \frac{5 \times 55}{8 \times 55} = \frac{275}{440}$
Glass: $\frac{2}{5} = \frac{2 \times 88}{5 \times 88} = \frac{176}{440}$
Scrap: $\frac{3}{4} = \frac{3 \times 110}{4 \times 110} = \frac{330}{440}$
Now, compare the numerators: 200, 275, 176, 330.
Arrange the numerators in descending order: 330, 275, 200, 176.
This corresponds to the fractions: $\frac{330}{440}$, $\frac{275}{440}$, $\frac{200}{440}$, $\frac{176}{440}$.
Replacing these with the original materials:
$\frac{330}{440}$ corresponds to Scrap ($\frac{3}{4}$).
$\frac{275}{440}$ corresponds to Aluminium cans ($\frac{5}{8}$).
$\frac{200}{440}$ corresponds to Paper ($\frac{5}{11}$).
$\frac{176}{440}$ corresponds to Glass ($\frac{2}{5}$).
The rate of recycling from greatest to smallest is: Scrap, Aluminium cans, Paper, Glass.
Answer:
(a) The amount of paper recycled is less than $\frac{1}{2}$.
(b) The items that have a recycled amount less than $\frac{1}{2}$ are Paper and Glass.
(c) The quantity of aluminium cans recycled is more than half of the quantity of aluminium cans.
(d) The rate of recycling the materials from the greatest to the smallest is: Scrap ($\frac{3}{4}$), Aluminium cans ($\frac{5}{8}$), Paper ($\frac{5}{11}$), Glass ($\frac{2}{5}$).
Question 147. The overall width in cm of several wide-screen televisions are 97.28 cm, $98\frac{4}{9}$ cm, $98\frac{1}{25}$ cm and 97.94 cm. Express these numbers as rational numbers in the form $\frac{p}{q}$ and arrange the widths in ascending order.
Answer:
Given:
The widths of four wide-screen televisions are 97.28 cm, $98\frac{4}{9}$ cm, $98\frac{1}{25}$ cm, and 97.94 cm.
To Find:
Express these numbers as rational numbers in the form $\frac{p}{q}$ and arrange them in ascending order.
Solution:
First, convert all the given widths into rational numbers in the form $\frac{p}{q}$.
1. 97.28 cm:
This is a terminating decimal. Write it as a fraction by placing the decimal part over a power of 10.
$97.28 = \frac{9728}{100}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor. Both are divisible by 4.
$\frac{9728 \div 4}{100 \div 4} = \frac{2432}{25}$
So, $97.28 = \frac{2432}{25}$.
2. $98\frac{4}{9}$ cm:
This is a mixed number. Convert it to an improper fraction.
$98\frac{4}{9} = \frac{(98 \times 9) + 4}{9} = \frac{882 + 4}{9} = \frac{886}{9}$
So, $98\frac{4}{9} = \frac{886}{9}$.
3. $98\frac{1}{25}$ cm:
This is a mixed number. Convert it to an improper fraction.
$98\frac{1}{25} = \frac{(98 \times 25) + 1}{25} = \frac{2450 + 1}{25} = \frac{2451}{25}$
So, $98\frac{1}{25} = \frac{2451}{25}$.
4. 97.94 cm:
This is a terminating decimal. Write it as a fraction by placing the decimal part over a power of 10.
$97.94 = \frac{9794}{100}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor. Both are divisible by 2.
$\frac{9794 \div 2}{100 \div 2} = \frac{4897}{50}$
So, $97.94 = \frac{4897}{50}$.
The widths as rational numbers in the form $\frac{p}{q}$ are:
$\frac{2432}{25}$, $\frac{886}{9}$, $\frac{2451}{25}$, $\frac{4897}{50}$.
Now, arrange these widths in ascending order (from smallest to largest).
To compare the fractions, find a common denominator. The denominators are 25, 9, 25, and 50.
LCM(25, 9, 50) = LCM($5^2, 3^2, 2 \times 5^2$) = $2 \times 3^2 \times 5^2 = 2 \times 9 \times 25 = 18 \times 25 = 450$.
Convert each fraction to have a denominator of 450:
1. $\frac{2432}{25} = \frac{2432 \times 18}{25 \times 18} = \frac{43776}{450}$
2. $\frac{886}{9} = \frac{886 \times 50}{9 \times 50} = \frac{44300}{450}$
3. $\frac{2451}{25} = \frac{2451 \times 18}{25 \times 18} = \frac{44118}{450}$
4. $\frac{4897}{50} = \frac{4897 \times 9}{50 \times 9} = \frac{44073}{450}$
Now, compare the numerators: 43776, 44300, 44118, 44073.
Arrange the numerators in ascending order: 43776, 44073, 44118, 44300.
This corresponds to the fractions: $\frac{43776}{450}$, $\frac{44073}{450}$, $\frac{44118}{450}$, $\frac{44300}{450}$.
Replacing these with the original widths:
$\frac{43776}{450}$ corresponds to $97.28$.
$\frac{44073}{450}$ corresponds to $97.94$.
$\frac{44118}{450}$ corresponds to $98\frac{1}{25}$.
$\frac{44300}{450}$ corresponds to $98\frac{4}{9}$.
The widths in ascending order are 97.28 cm, 97.94 cm, $98\frac{1}{25}$ cm, $98\frac{4}{9}$ cm.
Answer:
The widths as rational numbers in the form $\frac{p}{q}$ are:
$97.28 = \frac{2432}{25}$
$98\frac{4}{9} = \frac{886}{9}$
$98\frac{1}{25} = \frac{2451}{25}$
$97.94 = \frac{4897}{50}$
The widths in ascending order are:
97.28 cm, 97.94 cm, $98\frac{1}{25}$ cm, $98\frac{4}{9}$ cm.
Question 148. Roller Coaster at an amusement park is $\frac{2}{3}$ m high. If a new roller coaster is built that is $\frac{3}{5}$ times the height of the existing coaster, what will be the height of the new roller coaster?
Answer:
Given:
Height of the existing roller coaster = $\frac{2}{3}$ m.
The new roller coaster is $\frac{3}{5}$ times the height of the existing coaster.
To Find:
The height of the new roller coaster.
Solution:
To find the height of the new roller coaster, we need to multiply the height of the existing coaster by $\frac{3}{5}$.
Height of new roller coaster = $\frac{3}{5} \times (\text{Height of existing coaster})$
Height of new roller coaster = $\frac{3}{5} \times \frac{2}{3}$ m
Multiply the numerators and the denominators:
= $\frac{3 \times 2}{5 \times 3}$ m
We can simplify the multiplication by cancelling the common factor 3 in the numerator and the denominator.
= $\frac{\cancel{3}^1 \times 2}{5 \times \cancel{3}^1}$ m
= $\frac{1 \times 2}{5 \times 1}$ m
= $\frac{2}{5}$ m
So, the height of the new roller coaster will be $\frac{2}{5}$ metres.
Answer:
The height of the new roller coaster will be $\mathbf{\frac{2}{5}}$ metres.
Question 149. Here is a table which gives the information about the total rainfall for several months compared to the average monthly rains of a town. Write each decimal in the form of rational number $\frac{p}{q}$ .
| Month | Above / Below normal (in cm) |
|---|---|
| May | 2.6934 |
| June | 0.6096 |
| July | - 6.9088 |
| August | - 8.636 |
Answer:
Given:
The decimal values representing the deviation from average rainfall for different months are:
May: 2.6934
June: 0.6096
July: -6.9088
August: -8.636
To Find:
Express each decimal number as a rational number in the form $\frac{p}{q}$.
Solution:
To convert a terminating decimal to a rational number $\frac{p}{q}$, write the digits after the decimal point as the numerator and the denominator as a power of 10 corresponding to the number of decimal places, then simplify the fraction.
May: 2.6934
The number has 4 decimal places.
$2.6934 = \frac{26934}{10000}$
Simplify the fraction by dividing the numerator and denominator by their greatest common divisor. Both are divisible by 2.
$\frac{26934}{10000} = \frac{26934 \div 2}{10000 \div 2} = \frac{13467}{5000}$
The fraction $\frac{13467}{5000}$ is in its simplest form as 5000 has only prime factors 2 and 5, and 13467 is not divisible by 2 or 5.
June: 0.6096
The number has 4 decimal places.
$0.6096 = \frac{6096}{10000}$
Simplify the fraction.
$\frac{6096}{10000} = \frac{6096 \div 2}{10000 \div 2} = \frac{3048}{5000}$
$\frac{3048}{5000} = \frac{3048 \div 2}{5000 \div 2} = \frac{1524}{2500}$
$\frac{1524}{2500} = \frac{1524 \div 2}{2500 \div 2} = \frac{762}{1250}$
$\frac{762}{1250} = \frac{762 \div 2}{1250 \div 2} = \frac{381}{625}$
The fraction $\frac{381}{625}$ is in its simplest form as 625 is $5^4$, and 381 is not divisible by 5 (prime factors of 381 are 3 and 127).
July: -6.9088
The number has 4 decimal places.
$-6.9088 = -\frac{69088}{10000}$
Simplify the fraction.
$-\frac{69088}{10000} = -\frac{69088 \div 2}{10000 \div 2} = -\frac{34544}{5000}$
$-\frac{34544}{5000} = -\frac{34544 \div 2}{5000 \div 2} = -\frac{17272}{2500}$
$-\frac{17272}{2500} = -\frac{17272 \div 2}{2500 \div 2} = -\frac{8636}{1250}$
$-\frac{8636}{1250} = -\frac{8636 \div 2}{1250 \div 2} = -\frac{4318}{625}$
The fraction $-\frac{4318}{625}$ is in its simplest form as 625 is $5^4$, and 4318 is not divisible by 5.
August: -8.636
The number has 3 decimal places.
$-8.636 = -\frac{8636}{1000}$
Simplify the fraction.
$-\frac{8636}{1000} = -\frac{8636 \div 2}{1000 \div 2} = -\frac{4318}{500}$
$-\frac{4318}{500} = -\frac{4318 \div 2}{500 \div 2} = -\frac{2159}{250}$
The fraction $-\frac{2159}{250}$ is in its simplest form as 250 has prime factors 2 and 5, and 2159 is not divisible by 2 or 5 (prime factors of 2159 are 17 and 127).
Answer:
The rational numbers in the form $\frac{p}{q}$ are:
May: $2.6934 = \frac{13467}{5000}$
June: $0.6096 = \frac{381}{625}$
July: $-6.9088 = -\frac{4318}{625}$
August: $-8.636 = -\frac{2159}{250}$
Question 150. The average life expectancies of males for several states are shown in the table. Express each decimal in the form $\frac{p}{q}$ and arrange the states from the least to the greatest male life expectancy.
State-wise data are included below; more indicators can be found in the “FACTFILE” section on the homepage for each state.
| State | Male % | $\frac{p}{q}$ form | Lowest terms |
|---|---|---|---|
| Andhra Pradesh | 61.6 | ||
| Assam | 57.1 | ||
| Bihar | 60.7 | ||
| Gujarat | 61.9 | ||
| Haryana | 64.1 | ||
| Himachal Pradesh | 65.1 | ||
| Karnataka | 62.4 | ||
| Kerala | 70.6 | ||
| Madhya Pradesh | 56.5 | ||
| Maharashtra | 64.5 | ||
| Orissa | 57.6 | ||
| Punjab | 66.9 | ||
| Rajasthan | 59.8 | ||
| Tamil Nadu | 63.7 | ||
| Uttar Pradesh | 58.9 | ||
| West Bengal | 62.8 | ||
| India | 60.8 |
Answer:
Given:
The average male life expectancies for several states are provided as decimal numbers.
To Find:
Express each decimal as a rational number in the form $\frac{p}{q}$ (in lowest terms) and arrange the states from the least to the greatest male life expectancy.
Solution:
We convert each decimal life expectancy into a rational number in the form $\frac{p}{q}$.
Andhra Pradesh: $61.6 = \frac{616}{10} = \frac{308}{5}$
Assam: $57.1 = \frac{571}{10}$
Bihar: $60.7 = \frac{607}{10}$
Gujarat: $61.9 = \frac{619}{10}$
Haryana: $64.1 = \frac{641}{10}$
Himachal Pradesh: $65.1 = \frac{651}{10}$
Karnataka: $62.4 = \frac{624}{10} = \frac{312}{5}$
Kerala: $70.6 = \frac{706}{10} = \frac{353}{5}$
Madhya Pradesh: $56.5 = \frac{565}{10} = \frac{113}{2}$
Maharashtra: $64.5 = \frac{645}{10} = \frac{129}{2}$
Orissa: $57.6 = \frac{576}{10} = \frac{288}{5}$
Punjab: $66.9 = \frac{669}{10}$
Rajasthan: $59.8 = \frac{598}{10} = \frac{299}{5}$
Tamil Nadu: $63.7 = \frac{637}{10}$
Uttar Pradesh: $58.9 = \frac{589}{10}$
West Bengal: $62.8 = \frac{628}{10} = \frac{314}{5}$
India (Overall): $60.8 = \frac{608}{10} = \frac{304}{5}$
Now, we arrange the states in ascending order based on their life expectancies (from least to greatest).
The given decimal values in ascending order are:
56.5, 57.1, 57.6, 58.9, 59.8, 60.7, 60.8, 61.6, 61.9, 62.4, 62.8, 63.7, 64.1, 64.5, 65.1, 66.9, 70.6.
The corresponding states in ascending order of male life expectancy are:
Madhya Pradesh (56.5)
Assam (57.1)
Orissa (57.6)
Uttar Pradesh (58.9)
Rajasthan (59.8)
Bihar (60.7)
India (60.8)
Andhra Pradesh (61.6)
Gujarat (61.9)
Karnataka (62.4)
West Bengal (62.8)
Tamil Nadu (63.7)
Haryana (64.1)
Maharashtra (64.5)
Himachal Pradesh (65.1)
Punjab (66.9)
Kerala (70.6)
Answer:
The life expectancies as rational numbers in lowest terms are provided above.
The states arranged from the least to the greatest male life expectancy are:
Madhya Pradesh, Assam, Orissa, Uttar Pradesh, Rajasthan, Bihar, India, Andhra Pradesh, Gujarat, Karnataka, West Bengal, Tamil Nadu, Haryana, Maharashtra, Himachal Pradesh, Punjab, Kerala.
Question 151. A skirt that is $35\frac{7}{8}$ cm long has a hem of $3\frac{1}{8}$ cm. How long will the skirt be if the hem is let down?
Answer:
Given:
Current length of the skirt = $35\frac{7}{8}$ cm.
Length of the hem = $3\frac{1}{8}$ cm.
To Find:
The length of the skirt if the hem is let down.
Solution:
When the hem of the skirt is let down, the length of the hem is added to the current length of the skirt to get the new total length.
New length of the skirt = Current length + Length of the hem.
Substitute the given values:
New length = $35\frac{7}{8}$ cm + $3\frac{1}{8}$ cm.
We can add the whole number parts and the fractional parts separately, or convert the mixed numbers to improper fractions first.
Method 1: Add whole numbers and fractions separately.
Whole numbers: $35 + 3 = 38$
Fractional parts: $\frac{7}{8} + \frac{1}{8}$
Since the denominators are the same, add the numerators:
$\frac{7}{8} + \frac{1}{8} = \frac{7+1}{8} = \frac{8}{8} = 1$
Add the sum of whole numbers and the sum of fractional parts:
New length = $38 + 1 = 39$ cm.
Method 2: Convert to improper fractions.
$35\frac{7}{8} = \frac{(35 \times 8) + 7}{8} = \frac{280 + 7}{8} = \frac{287}{8}$
$3\frac{1}{8} = \frac{(3 \times 8) + 1}{8} = \frac{24 + 1}{8} = \frac{25}{8}$
Add the improper fractions:
New length = $\frac{287}{8} + \frac{25}{8} = \frac{287 + 25}{8} = \frac{312}{8}$
Simplify the resulting fraction by dividing the numerator by the denominator:
$\frac{312}{8} = 39$
Both methods give the same result.
The new length of the skirt will be 39 cm.
Answer:
If the hem is let down, the skirt will be 39 cm long.
Question 152. Manavi and Kuber each receives an equal allowance. The table shows the fraction of their allowance each deposits into his/her saving account and the fraction each spends at the mall. If allowance of each is Rs. 1260 find the amount left with each.
| Where money goes | Fraction of allowance | |
|---|---|---|
| Manavi | Kuber | |
| Saving Account | $\frac{1}{2}$ | $\frac{1}{3}$ |
| Spend at mall | $\frac{1}{4}$ | $\frac{3}{5}$ |
| Left over | ? | ? |
Answer:
Given:
Total allowance for Manavi = $\textsf{₹}1260$.
Total allowance for Kuber = $\textsf{₹}1260$.
Manavi's fraction saved = $\frac{1}{2}$.
Manavi's fraction spent = $\frac{1}{4}$.
Kuber's fraction saved = $\frac{1}{3}$.
Kuber's fraction spent = $\frac{3}{5}$.
To Find:
The amount of money left with Manavi and Kuber individually.
Solution:
First, calculate the total fraction of allowance saved and spent by Manavi.
Total fraction used by Manavi = Fraction saved + Fraction spent
= $\frac{1}{2} + \frac{1}{4}$
Find a common denominator (LCM of 2 and 4 is 4):
= $\frac{1 \times 2}{2 \times 2} + \frac{1}{4} = \frac{2}{4} + \frac{1}{4} = \frac{2+1}{4} = \frac{3}{4}$
The fraction of allowance left with Manavi is the total allowance fraction (which is 1) minus the fraction used.
Fraction left with Manavi = $1 - \frac{3}{4} = \frac{4}{4} - \frac{3}{4} = \frac{1}{4}$
The amount left with Manavi is this fraction multiplied by the total allowance.
Amount left with Manavi = $\frac{1}{4} \times \textsf{₹}1260$
= $\textsf{₹}\frac{1260}{4}$
= $\textsf{₹}315$
Next, calculate the total fraction of allowance saved and spent by Kuber.
Total fraction used by Kuber = Fraction saved + Fraction spent
= $\frac{1}{3} + \frac{3}{5}$
Find a common denominator (LCM of 3 and 5 is 15):
= $\frac{1 \times 5}{3 \times 5} + \frac{3 \times 3}{5 \times 3} = \frac{5}{15} + \frac{9}{15} = \frac{5+9}{15} = \frac{14}{15}$
The fraction of allowance left with Kuber is the total allowance fraction (which is 1) minus the fraction used.
Fraction left with Kuber = $1 - \frac{14}{15} = \frac{15}{15} - \frac{14}{15} = \frac{1}{15}$
The amount left with Kuber is this fraction multiplied by the total allowance.
Amount left with Kuber = $\frac{1}{15} \times \textsf{₹}1260$
= $\textsf{₹}\frac{1260}{15}$
To simplify $\frac{1260}{15}$, we can divide both numerator and denominator by common factors (e.g., 5 and then 3, or 15 directly).
$\frac{1260}{15} = \frac{\cancel{1260}^{252}}{\cancel{15}_{3}} = \frac{252}{3} = 84$
So, Amount left with Kuber = $\textsf{₹}84$
Answer:
The amount left with Manavi is $\textsf{₹}315$.
The amount left with Kuber is $\textsf{₹}84$.

